
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи узловых проводимостей дуальной схемы {(р=0) Yi + Y, + Y, -Y, Ys ~Y, Y+Y,+ Y -Y, - -Кз -К, y + Ys+Yj Приравнивая вначале соответствуюшие внедиагональные элементы матриц 2 ! и УУ>, определим следующие параметры дуальной схемы: K8=Z3-Z,4; Y,Zi-Z; Y,=Z,+Zi,+Zs- Из сравнения соответствующих диагональных элементов матриц Z и уУ * получим: yi = Zi+Z3+ZB-(Z3-Zi4)-(Z6 + ZM + Z29) = Zi-Za9; Y2=Z+Zt+Zs-{Zi~-Z)-{Z+Zu+Z)===Z-Zut Y=Z+Zs+Z-(Zs-Zu)~iZi-Z) = Z+Zi+Zs- В исходной схеме матрица контурных э. д. с. Ш> = [0 О no3TOjqr в дуальной схеме необходимо включить источниктока J = S межДу базисным узлом 4 и узлом 3. Матрица узловых токов дуальной схемы jcy) i=[0 О Jf = g(Ki. Приведенные выражения для проводимостей дуальной схемы показывают, что индуктивным (емкостным) сопротивлениям исходной схемы соответствуют емкостные (индуктивные) проводимости в дуальной схеме. 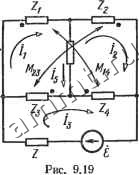 Рис. 9.20 С помощью дуальных схем для цепей с взаимной индукцией можно применять топологические методы анализа и методы преобразования схем. Пример 9.5. Определить ток Д в схеме на рис. 9.19. Решение. Ток /5 найдем с помощью дуальной схемы на рис. 9.20. В исходной схеме ток /б = /1 -4- Контурные токи 4 и 4 равны соответственно потенциалам Ф1 и фа дуальной схемы. Включив вольтметр между узлами 1-2, определим разность ф!-Фа где nkAkYY-YiYi. 1-3: Определитель Д вычислим с помощью разложения по путям между узлами Д = УгУ (Vs-bП+ П) + УлУгУ + УьУУ + УьУ(Vi+ У2+У) + + Ув {У г {У+Уь+У1+У)+У+Yi) (У*+Уь)Ь Таким образом. Подставляя соотношения для проводимостей дуальной схемы (см. пример 9.4) и заменяя / на , выразим ток /в через параметры исходной схемы. Дуальные схемы могут быть применены и для моделирования процессов в цепях с индуктивными связями с помощью цепей без индуктивных связей. § 9.5. Расчет цепей с невгаимными злементамн Матричные уравнения *. В различных областях техники широкое применение находят электрические цепи, содержащие трехполюсные элементы - электронные лампы и транзисторы. Принцип действия электронной лампы и транзистора, их основные уравнения в линейном режиме и эквивалентные схемы для переменных составляющих напряжений и токов были рассмотрены в гл. 1 (см. § 1.8). Цепи с электронными лампами и транзисторами содержат источники постоянной и переменной э. д. с. (тока). В линейном режиме при расчете переменных составляющих напряжений и токов источники постоянной э. д. с. исключаются (замыкаются). Постоянные составляющие напряжений и токов позволяют определить параметры эквивалентных схем для переменных составляющих (далее эти параметры предполагают заданными). Трехполюсный элемент (рис. 9.21, а) можно характеризовать уравнениями (для гармонических переменных составляющих) 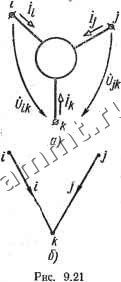 Yu LYfi Zii ZuA (9.19) (9.20) Переменными составляющими в уравнениях (9.19) и (9.20) служат токи зажимов /, / трехполюсника и напряжения между зажимами i - k, l - k. Зажим k, относительно которого отсчитывают напряжения Uik, Ojk, называют базисным зажимом. Если зажим i рассматривают как входной, а зажим / - как выходной зажимы трехполюсника, то зажим k назьшают также общим зажимом (по отношению к входу и выходу). * В данной главе рассматриваются особенности расчета цепей с электронными трехполюсниками в предположении линейности их режима.
Матрицы в уравнениях (9.19) и (9.20) представляют собой определенные матрицы параметров трехполюсника при базисном зажиме k (матрицу проводимостей и матрицу сопротивлений) *, причем Y = = Z- и Z = Y-. Если зажим / совпадает с зажимом сетки, зажим / - с зажимом анода, а зажим k - c зажимом катода лампы, то в соответствии с уравнениями (1.18) матрица проводимостей лампы О О L5 gi\ (9.21) Матрица (9.21) является особенной (ее определитель равен нулю), следовательно, матрица Z = Y~ не существует. Если зажим i совпадает с зажимом эмиттера, зажим / - с зажимом коллектора, а зажим k - c зажимом базы транзистора, то в соответствии с уравнениями (1.21) матрица сопротивлений транзистора (9.22) Вьиисляя матрицу, обратную матрице (9.22), можно получить матрицу проводимостей транзистора: б + -к -Гб L-(б + агк) Гв + б. (9.23) А = (в + б){/-б + к) - г6(/-б + а/-к) = /-а(Гк + /-б) + (1 - оС)Г(,г. (9.23а) С помощью матриц Y и Z трехполюсника могут быть составлены узловые и контурные уравнения или уравнения с напряжениями ветвей дерева (7.27)(7.29). Для этого каждый трехполюсник (рис. 9.21, а) заменяют его графом (рис. 9.21, б), двухполюсные ветви схемы - отрезками линий. Для полученного графа цепи составляют матрицы А, В или Q. В матрице проводимостей ветвей Y (сопротивлений ветвей Z )) на главной диагонали записываются проводимости F/ (сопротивления Z/) двухполюсных ветвей, проводимости Уц, Yj/ (сопротивления Zn, Z/j), соответствующие ветвям i и / графа трехполюсника с базисным зажимом k (рис. 9.21, б); вне главной диагонали записывают проводимости Yif, Yfi (сопротивления Zy, Z,-,-). Матрицы узловых проводимостей, проводимостей сечений, контурных сопротивлений. * Матрицы Y и Z трехполюсников в общем случае отличаются от матриц узловых проводимостей и контурных сопротивлений. Матрицу Y называют матрицей проводимостей короткого замыкания (при коротко-замкнутых зажимах), а матрицу Z-матрицей сопротивлений при разомкнутых зажимах.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
|
|