
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи положительным направлениям напряжении относительно Соответствующих точек на схеме. Напряжение 724 = Ф2 -Ф4 (рис. 7.11) (направленное от точки 2 к точке 4) направлено от точки 4 к точке 2, что объясняется правилом вычитания векторов: разность векторов всегда направлена в сторону уменьшаемого вектора. При построении топографических диаграмм разветвленной цепи можно также показать векторы токов в ветвях, векторы всех э. д. с. и токов источников токов. J10M -J0.5DH 2 3 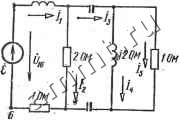 S . 4 Пример 7.4. На рис. 7.13 изображена схема электрической цепи и указаны . Определить токи во всех ее параметры. Определить ветвях схемы и напряжение f7=#, если Рис. 7.13 ток /5=1 А. Построить топографическую диаграмму и векторную диаграмму токов. Решение. Если вектор тока 4 направить по оси вещественных величин (/5=75=1 А) а потенциал точки 4 принять равным нулю (ф4=0), то фз = = ф4+1-/в=1 В. Ток /4=1 2=-/0,5 А, а ток /з=/4+/д= 1-/0,5 А. Потенциал ф2=Фз+( -/0,5)/3= 1 -/0,5 (1 -/0,5) = 0,75-/0,5 В, потенциал Ф5=Ф4-(-/0,5)/8=/0,5(1-/0,5)=0,25-Ь/0,5 В. Разность потенциалов узлов 2 и 5 £45=Ф2-Фб=(0.75-/0,5)-(0,25-Ь/0,5) =0,5-/ В, следовательно, - 4=tW2=0,25-/0,5 А; /i=/2-f/g=0.25-/0.5-j-/-A5=l,25-/ А. Найдем потенциалы фд и ф: Ф1=Ф2+/1 /i=(0,75-/0.5)-l-/(1.25-/)=1,75-Ь/0,75 В; Фв=Фв-Ь/1=0.25-Ь/0,5-1,25+/=-1/1,5 В. Напряжение f/= =ф1-фв= 1,75+/0,75 + 1-/1,5 = 2,75-/0,75 В. На рис. 7.14 построены топографическая диаграмма и векторная диаг-рамма токов. 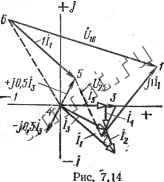 -ХгЧВОм 4 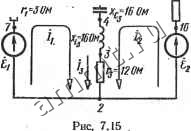 Пример 7.5. На рис. 7.15 изображена схема электрической цепи и указаны ее параметры. Определить токи в вегвях схемы с помощью контурньи и узловых уравнений, если #j;= ISOe В, =220е В. Построить топографическую диаграмму и векторную диаграмму токов Решение. Kl онтурные уравнения схемы имеют вид (Zi+2з) h + 2з4=15 Zsh+{2а+Z3) 4 = +Zg=3+/ (8 - 4) +12+/ (32 -16) = 15+/20 Ом, 2з=12+/(32-16)=12+/16 Ом. Z2+Z3=6+/(16-8)4-lf+/{32-16}=18+/24 Ом. Запишем эти уравнения следующим образом; (15 + /20)/i + {12 + /16) 4=120е3<°; (124-/16)/х4-(18+/24) 4==220е3<° 25е/53.1-д+20e/53.l-4= 120е/зе ; 20e53- /i+30е53->72=220е30°. Решая два уравнения совместно, получим: Л=-2.28е-/23.1- д. 4=8.86е-23.1- А; /д=Д+/,=6.58е-23.1- А, Заданная схема имеет два узла, поэтому при ф2=0 для потенциала щ справедливо уравнение * откуда + 1.1.1 Токи ветвей определим из выражений Zi 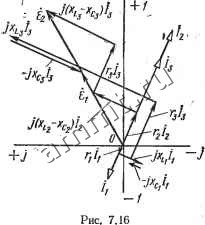 На рис. 7.16 построены топографическая диаграмма напряжений и векторная диаграмма токов. § 7.5. Основные свойства и преобразования цепей о источниками гармонических э. д. с. и токов Основные свойства цепей. В электрической цепи, содержащей источники гармонических э. д. с. и токов, для мгновенных мощностей ветвей выполняется соотношение h А=1 (7.36) 203 доказательство которого совпадает с доказательством равенства (5.1), Так как комплексные действующие значения токов ветвей удовлетворяют уравнению А1) = 0, справедливо уравнение -А !< ) = О, где Г ) -матрица комплексных величин, сопряженных с комплексными действующими значениями токов ветвей. С помощью последнего уравнения легко доказать соотношения: (7.37) (7.38) (7.39) где 1г = [/zj - матрица токов в сопротивлениях ветвей Zj,. Доказательство равенств (7.37)-г-(7.39) аналогично доказательству выражений (5.1), (5.4), (5.5). Равенства (7.37), (7.38) представляют собой математическую формулировку баланса комплексных мощностей. В правой части равенства (7.39) записана сумма комплексных мощностей, генерируемых источниками э. д. с. и тока: fe=i ft=i fe=i k=\ Подставляя в левой части равенства (7.39) вместо Z сумму Rk-{-jXk и приравнивая соответственно вещественные и мнимые части равенства, можно получить: 2 Ih = S /исх; (7.40) k=i fe=i 2 XkfZk ~ Е йист-й=1 ft=l (7.41) Таким образом, в цепи с гармоническими э. д. с. и токами выполняется баланс активных и реактивных мощностей: активная мощность, генерируемая источниками энергии, равна активной мощности, рассеиваемой в сопротивлениях г; реактивная мощность источников энергии равна реактивной мощности в реактивных сопротивлениях Xk (реактивная мощность ин-дуктивностей учитывается с положительным знаком, а емкостей -с отрицательным). Принцип наложения, свойство взаимности, теоремы о компенсации и об эквивалентном источнике (см. гл. 5) справедливы и для цепей с гармо-.ническими э. д. с. и токами. Математические соотношения для 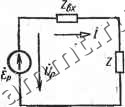 Рис. 7.17
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |