Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [ 27 ] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ГЛАВА 4

АЛГЕБРАИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ЦЕПЕЙ ПРИ УСТАНОВИВШЕМСЯ РЕЖИМЕ

§ 4Л. Применение уравнений Кирхгофа

Матричная форма закона Ома. Каждая ветвь цепи может содержать сопротивление г и, идеальный источник э. д. с. и идеальный источник тока Ju, где k=\, 2, в (рис. 4.1, с). Иногда источники тока на схеме не изображают, а показывают только токи источников в соответствующих узлах (рис. 4.1, б). - Ток в сопротивлении (рис. 4.1)

/г h + Jk, где /ft -ток k-u ветви.

Потенциал ф узла п отличается от потенциала узла т : на величину падения напряжения в сопротивлении и на зна-

к I,

Рис. 4.1

чение э. д. с. (f, причем для указанных положительных направлений падение напряжения уменьшает, а э. д. с. увеличивает потенциал ф:

Напряжение на зажимах ветви ,

откуда , - .

Uk = n{h + Jk)-<k. (4.1)

Соотношения для токов:

h-gki.Uk-k)-Jk, (4.2)

где gfe=l/rft -проводимость ветви.

Формулы (4.1) и (4.2) представляют собой аналитические выражения закона Ома для участка цепи с источниками э. д. с. и тока.

в общем случае, если ветвь содержит ряд последовательно соединенных сопротивлений, источников э. д. с. и параллельно соединенных источников тока, то в формулах (4.1) и (4.2) вместо /- следует учитывать суммарное сопротивление ветви, а вместо и У -алгебраическую сумму соответственно э. д. с. источников э. д. с. и токов источников тока. При этом с положительным знаком записывают э. д. с. и токи источников, ориентированные относительно тока так, как показано на рис. 4.1 *; при противоположных направлениях э. д. с. и токи источников записывают с отрицательными знаками.

Пример 4.1. С помощью закона Ома определить токи на всех участках цепи на рис. 4.2, а и построить график распределения потенциала (потенциальную диаграмму) вдоль замкнутого контура. Параметры схемы: г1 = г~ = 2 Ом; /-3 = 5 Ом; /-4=1 Ом; eie\ = W В; (fa=-20 В; Ji=lQ А.

Решение. Схему на рис. 4.2, а рассмотрим как параллельное соединение двух ветвей, присоединенных к узлам / и 5. Одна ветвь содержит элементы fi, el и Ji, другая -гг, гз, г, и (93. По закону Ома для первой ветви справедливо уравнение

Viri[li-Ji)-ei

Для второй ветви

i=2t/i-10)-f 10 = 2/1-10,

t2 = z2-®z,

где , = t-r-r; 2 =<2 + <з,

6/2=8/2-1-10.

Так как i/j = i/2, i = 2 А; /3 = -2 А; / = /-У=-8 А.-

Для построения потенциальной диаграммы вычислим потенциалы точек контура, отмеченных цифрами 1 - 7. Пусть ф1 = 0, тогда

ф2 = Фг + <1=0+10.= 10 В;

Pз=P2+l. = 10-8=-6 В;

ф4=Фз--24=-6 + 2 . 2=-2 В;

Фб=Ф4 + 2 = -2-20 = -22 В;

Фв = Фб-гз4 = -22-f5.2 = -12 В;

Ф7=фв+з=-12-1-10=-2В.

Обход контура заканчивается в узле /, потенциал которого

ф1 = ф-4/3=-2-f 1. 2 =0,

как и было принято ранее.

При построении потенциальной диаграммы по оси абсцисс откладываем в определенной последовательности сопротивления участков, а по оси ординат-потенциалы соответствующих точек (рис. 4.2, б).

Пользуясь графиком распределения потенциала, определяем напряжения между любыми точками схемы. Например, напряжение 6/г5 = ф2 -ф5=32 В; /47 = ф4-Ф; = 0 и т. д.

* Положительные направления t, /,- и принимают совпадающими и,

как правило, указывают одной стрелкой на соответствующей ветви графа. 86

Отношение падения напряжения на сопротивлении к сопротивлению равно току участка и на графике определяется как тангенс угла наклона соответ-ствуюш,ей прямой к оси абсцисс. Поэтому наклон прямых {3-4, 5-6, 7-1 на рис. 4.2,.б), отображающих изменение потенциала вдоль сопротивлений с одним в тем же током /а, одинаков.

Соотношение (4.1) запишем для всех в ветвей в виде матричного равенства .

/2 +л

(4.3)

- диагональная матрица сопротивлений ветвей (все элементы этой матрицы, за исключением элементов главной диагонали, равны нулю; элемент, находящийся на пересечении k-u строки и -го столбца, равен сопротивлению k-u ветви /-ft);

1 = [/1/2.../еГ.

- соответственно векторы напряжений и токов ветвей, токов источников тока и э. д.с. источников э. д. с. ветвей.

На основании выражения (4.2) запишем матричное соотношение

(44)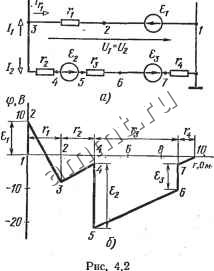

- диагональная матрица проводимостей ветвей. В этой матрице элемент = Цг, поэтому матрицы R * и ОС - взаимно обратны.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [ 27 ] 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.