Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 [ 53 ] 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

Реактивная мощность

Q = UI smq>, полная мощность

Мощность, рассеиваемая в сопротивлении г, = t/,/= гЯ = t cos ф = Р,

т. е. вся активная мощность, потребляемая цепью, рассеивается в сопротивлении. Реактивная мощность индуктивности

= t/i/= = t sin ф = Q.

Параллельная цепь. Если к источнику гармонического тока /(;) = J sin (©/ + ];) подключается сопротивление г и индуктивность L (рис. 6.14), то при разомкнутом ключе справедливо уравнение

Дифференцируя это уравнение по времени, получаем

T + UXLJmSin(<0t-{-i+fj. (6.26)

Уравнение (6.26) аналогично уравнению (6.19), поэтому для напряжения и можно сразу записать выражение, аналогичное (6.22):

иЛе-/-f t/ sin(co/-bij5 ), (6.27)

где Um = Jm; a~+Y~ (6 = arctgxi/r). Если сопротивления г и Xl заменить их обратными величинами g и bi, то

где y = Vg + bl; ф = -6 = arctgbi/g.

Так как в момент размыкания ключа гх(0) = 0, напряжение

(0) = r/(0) + rJ sinil.

Следовательно, постоянная интегрирования А определяется из условия

u(0) = A + Usin% = rJmSin\ii,

откуда Л =r/msinij) -f/m sinijj . Окончательное выражение для напряжения имеет вид

is У

sinijj-81п(11з-Ьф) e-/ + -sin(c3/-fil)-l-q)). (6.28)

Экспоненциальная составляющая в правой части (6.28) представляет собой свободное напряжение ев а гармоническая - при-

нужденное напряжение и р. На рис. 6.15 показаны графики функций Ыев* пр. для случая il) = 0, 0<ф<Я/2. Ток в сопротивлении

ir = g = sinij; -1- J г Sin + ф)1 е / + fj , sin (со/+iJj + ф),

. (6.29)

ток в индуктивности

jii = J d/= ут81п(т1) + ф)-У 81п11з е-А +

+ sin(a> + г + ф--). (6.30)

При определении тока ii постоянная интегрирования принята равной нулю, так как в данном случае ток h не мoжeт содержать nocTojfHHOft составляющей. Выражение (6.30) удовлетворяет условию ti(0)==0 и ir + ii- =J (t). Ток ii может быть найден и как разность J (t) - i.

При установившемся режиме токи ir, il и напряжение и не

J(t)\

\,1г i к

Рис. 6.14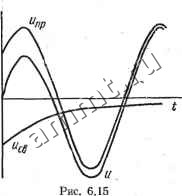

содержат свободных составляющих. Для такого режима справедливы выражения:

и=sin(ш/ + яJ) + ф); (6.31)

iV=--f-msin(fi)/-f г1) + ф);

Ь, I л\

= - J sin(©-1-11) -f ф -Y

(6.32) (6.33)

Напряжение при установившемся режиме и опережает ток в неразветвленной цепи i = J{t) на угол Ф = iJJh -Ф/=Фи -Ф. который зависит от соотношения между активной (g) и индуктивной (bi) проводимостями:

О Ф = arctg bi/g я/2.

Ток ir совпадает по фазе с напряжением и, а ток it отстает от напряжения и на угол я/2. На рис. 6.16 приведены зави-

симости и, ir, h, i = J от времени в принужденном режиме, а на рис. 6.17 показана векторная диаграмма рассматриваемой цепи. Вектор / = / равен сумме векторов /, и ti, так как i==iV + i-Из векторной диаграммы легко установить соотношения между

действующими значениями токов: Ir = I COS ф; /1 = /5Шф.

Величину у =l/g-f fcl называют полной проводимостью рассматриваемой цепи. С помощью проводимости у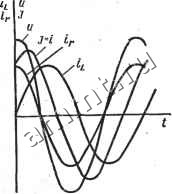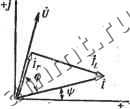

Рис. 6.16

Рис. 6.17

связь между амплитудами напряжения Um и тока = Jm выражается аналогично закону Ома:/Ут=/от/</. Так как ф = arctg-~; =

= /со8ф; Ьi = /siпф.

При установившемся режиме активная мощность, потребляемая цепью:

Р = -

реактивная мощность полная мощность

cos ф = /7/ со8ф; С = [ 8тф;

Мощность, рассеиваемая в сопротивлении, Pr = Ul,gU = Ul cos({> = P, реактивная мощность индуктивности

= = bit/ =/7/sin ф = Q.

§ 6.5. Цепи с сопротивлением г и емкостью С

Последовательная цепь. На рис. 6.18 изображена последовательная гС-цепь, подключаемая к источнику э. д. с. Эта цепь дуальна цепи на рис. 6.14, поэтому выражения для тока i, на-

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 [ 53 ] 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.