
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Из уравнения (14.9) получаем cos&=l - При ю = CXD & = о, при со = (Во COS Ь = - 1, следовательно, Ь = - я. Характеристические сопротивления для Т- и П-образных схем определяются по формулам 2.r= lL/CVl-(cog/co2); 2ся = VVC iV 1 - (со/со))- (14.17) На рис. 14.10,2 построены графики зависимости характеристических сопротивлений Ест и от ю/соо. В полосе пропуска- 0-НН 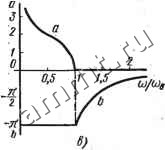 о 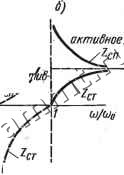 реактив] ное I инддк 1. Уное \емкостще Рис. 14.10 ния эти сопротивления являются активными. При этом если сопротивление 1сп изменяется от оо до У L/C, то сопротивление ZcT от О до У LjC. Для согласования фильтра с нагрузкой сопротивление нагрузки должно быть активньм и меняющимся при изменении частоты в соответствии с кривыми на рис. 14.10, г. В полосе задерживания характеристические сопротивления Есп и ZcT являются реактивными и имеют разные знаки, причем сопротивление Zen носит индуктивный, а сопротивление Zct - емкостной характер. Полосовые (полосные) фильтры. Если схемы фильтра на рис. 14.7 и рис. 14.9 как бы электрически совместить друг с другом, то полученный фильтр будет пропускать сигналы в диапазоне изменения частоты от coj, до cog. На рис. 14.11, а, б изобра- зкены две такие схемьт, имеющие соответственно Т- и ГГ-образные формы. Чтобы при одной и той же частоте стали равны нулю продольные сопротивления Z (резонанс напряжений) и попереч- 2С 2С 0 orJ L-j L.non 0 0 г -ю 1. X Уг/2 Сг/2 Рис. 14.11 ные проводимости Y (резонанс токов), необходимо выполнить условие, определяющее частоту , . при котором LiCiLzCi. При рассмотрении схем на рис. 14.П,с, б с учетом уравнения (14.18) можно получить выражения для Z и F в виде (14.19) Уравнение, определяющее границы полосы пропускания фильтра, имеет вид . Одним из решений этого уравнения является уже найденная частота coq. Остается решить уравнение \ Юо ю у (14.20) со ± 2ш,1 У LgCi - со? = 0. Если опустить отрицательное значение частоты, как не имеющее смысла, то coi = a)o(K +l-n); (14.21) Из полученных выражений следует, что фильтр пропускает сигналы при изменении частоты от coi до cog (рис. 14,12, а). Частота соо оказывается промежуточной, поскольку она равна среднему геометрическому из граничных частот, т. ё. ft)o = K< iW2 f Ы/Ыд Ы/Ыд 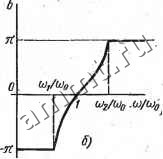 Рис. 14.12 Частотнур зависимость коэффициента затухания а в полосе подавляемых частот находим с помощью выражения chc = 2Ci \щ (й ) (14.22) По этому уравнению на рис. 14.12, а построена частотная характеристика а {(о/щ) для рассматриваемого полосового фильтра. Зависимость коэффициента фазы b в полосе пропускания определяем по соотношению (14.23) При изменении частоты от соо ДО щ характеристика b {(о/щ) аналогична фазовой характеристике, фильтра нижних частот (см., рис. 14.8, а), коэффициент b меняется от О до я (рис. 14.12,6). При изменении частоты от coi до соо характеристика &(о)/шо) аналогична фазовой характеристике фильтра верхних частот, при этом b изменяется от -я до 0. Для получения более полной характеристики режима работы полосового фильтра необходимо выяснить закон изменения характеристических сопротивлений в обеих схемах (см. рис. 14.11, с, б). Характеристические сопротивления полосовых Т- и П-образных фильтров можно найти с помощью общих уравнений (14.11) и (14.12). Пользуясь этими уравнениями и учитывая (14.19), получим: \<йо (14.24) (14.25)
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |