Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 [ 80 ] 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

В соогветствии с рис. 8.18, в коэффициент передачи тока

Acs- д .

1 1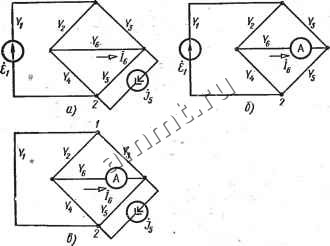

Рис. 8.18

Знаменатель Д функций и Иь найдем с помощью разложения по путям между узлами /, 2 (рис. 8.18, а) при исключенных-источниках:-

Д= 2 ЛДй,

Я, = К,; Ax-(Y2+Y)(Y+Ys+Y) + Y{Y3+Yy. .

- . /7,= К,Г4; AYa+Y+Y,

.Яз = К2КвК5; Дз = 1;

/74=Узв4: Д4=1: , . .

ЩУзУ; Д5 = Г,+ К4 + Кв.

Подстановка значений Yi и в выражение для тока приводит к искомому результату.

§ 8.5. Топологические формулы для расчета контурного определителя и алгебраических дополнений его элементов

Топологическую формулу для определителя А< * матрицы контурных сопротивлений Z* , называемого контурным опреде-

л и те л ем, можно получить на основании выражения Д<> = det [BZC>B-] = det (PiPa).

где Pi = BZ< ); PaB.

Если матрица В записана для главных контуров произвольной схемы, то ненулевые миноры порядка к = в - у+1 этой матрицы соответствуют ветвям связи (дополнениям деревьев) и равны dt 1 (см. гл. 2). Это утверждение справедливо и для миноров матрицы В планарной схемы цри условии, что контуры выбраны в виде ячеек. Ненулевые миноры порядка к матрицы Pi = BZ также соответствуют ветвям связи деревьев и равны взятым с положительным (отрицательным) знаком произведениям сопротивлений соответ-ствукхцих ветвей связи.

Применяя теорему Бине-Коши к определителю произведения матриц Pi = BZ<) и Р2 = В-, можно найти

Д(к) . 2 Z/iZ/2 ... Zy,b y4.i,

(8.16)

т. е. контурный определитель равен сумме произведений сопротивлений ветвей связи для всех деревьев.

Из формулы (8.16) следует важный вьюод: для любой системы главных контуров произвольной схемы контурный определитель имеет единственное значение. Если схема планарная, то контурный определитель имеет единственное значение для любой системы главных контуров и для контуров, выбранных в виде ячеек.

В случае, когда контуры не являются главными контурами или ячейками планарной схемы, значение контурного определителя отличается от значения, данного в формуле (8.16). При этом ненулевые миноры порядка

к матрицы В соответствуют ветвям связи деревьев и равны ±б. Где б - целое число, которое может быть больше единицы. Например, для схемы, граф которой приведен на рис. 8.19, можно выбрать независимые контуры, состоящие из ветвей /-7-9-S-8-5, 1-2-9-6-5, 2-3-4-5-6-7. 1-7-6-8-4. Эти контуры не представляют собой главные контуры или ячейки. Матрица таких контуров

:i О 1 О -1 О 1 10 0-1-1 0 111 1 1-1 10 0 1 О --1

Рис. 8.19

I -1

О -1

о о

Для дерева 5-6-7-8-9 ветвями связи являются ветви /-2-3-4. Соответствующий им минор матрицы В

1 О I О

110 0

О 11 1

10 0 1

det Bi234 =

= 3.

Следовательно, любой ненулевой минор четвертого порядка записанной матрицы равен ±б = ±:3.

Для контуров-ячеек 1-7-6-5, 2-9-7, 3-8-6-9, 4-5-8 матрица

Ч О О О -1 -1 1 О О 0 10 0 О 0-1 0-1 0 0 10 О 1 0-1 1 0 0 0 1 1 € 0 1 О

Минор, соответствующий ветвям связи 1-2-3-4, равен 1; все другиененулевые миноры четвертого порядка равны ±\. В данной схеме ячейки являются главными контурами по отношению к дереву 5-6-7-8-9.

Если ненулевые миноры порядка к матрицы В равны dh б (б 9 1), то определитель матрицы контурных сопротивлений Z< = BZ<°>B отличается от значения, приведенного в выражении (8.16), в 6 раз. Далее рассматриваются лишь матрицы В главных контуров произвольной схемы или контуров-ячеек планарной схемы; при этом 6 = 1 и для контурного определителя справедлива топологическая формула (8.16).

Следует установить связь между узловым определителем Д> и контурным определителем А< * одной и той же схемы. Для этого обе части равенства (8.1) умножаем на произведение сопро-

тивлений всех ветвей схемы Z. При умножении каждого

слагаемого правой части равенства (8.1) на YLZk српротивления

fe = i

ветвей каждого дерева сократятся с проводимостями ветвей. В результате в правой части получим сумму произведений сопротивлений ветвей связи деревьев, т. е. контурный определитель. Таким образом,

/в \

(8.17)

Аналогично устанавливается соотношение П Г)д( )==А(Ч

(8.18)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 [ 80 ] 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.