
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи графики изменения Раь, Реь и Р = Раь + Рсь при изменении (ю от О до ± 90°. На рис. 10.32 показана схема включения ваттметра с искусственной нейтральной точкой, позволяющая измерить активную мощность одной фазы симметричной трехфазной трехпроводной цепи. . Искусственная нейтральная точка создается из трех одинаковых активных сопротивлений. При этом в- Гд служит добавочным сопротивле- 0~ с нием, которое вместе с сопротивлением обмотки напряжения ваттметра должно равняться сопротивлению каждой из двух других фаз: Гд + --1&=- Суммарная активная мощность в этом случае равна утроенному значению мощности, показываемой одним ваттметром. На рис. 10.33, с изображена схема включения ваттметра, для измерения реактивной мощности симметричной трехфазной цепи. Из приведенной диаграммы iii iii iii Рис. 10.32 схемы и из векторной изображенной на рис. 10.33, б, следует, что ваттметр Uab. Рис. 10.33 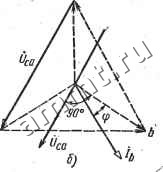 измеряет мощность UcJb cos (tOfi) = Ucbh cos (90° - Ф) = UJ sin ф, что при умножении на YZ дает реактивную мощность симметричной трехфазной цепи. § 10.6. Оснсвные понятия о методе симметричных составляющих Для расчета несимметричных режимов линейных многофазных цепей часто применяют метод симметричных составляющих, основанный на. принципе наложения. Этот метод позволяет упростить расчет несимметричного режима линейной трехфазной цепи в тех-случаях, когда причины нарушения симгжтрии (обрыв фазы, короткое замыкание и т. п.) сосредоточены в одном или двух местах системы; при этом все остальные ветви трехфазной цепи имеют одинаковые параметры всех фаз. В таких случаях вместо одной несимметричной трехфазной системы можно рассматривать три сигушетричные системы, схемы замещения которых составляются на одну фазу и соединяются между собой в соответствии с условиями, возникающими в местах нарушения симметрии. Любую несимметричную т-фазную систему некоторых величин А можно рассматривать как сумму т различных симметричных т-. фазных систем, различающихся значениями аргумента argAfe = = 6, [ = 0, 1, ... (m-1)]. Если для каждой k-я симметричной системы величину Аа для фазы А принять за исходную, то для любой другой фазы , . 2л *а = Лле -= е *. Таким образом, все системы получаются симметричньми, за исключением системы нулевой последовательности ( = 0), у кото- рой Лоа =-Лол = const, И в сумме составляют оа = -ол. т. е. представляют неуравновешенную систему. Таким образом, система нулевой последовательности является симметричной только по формальным признакам. Тогда для каждой фазы несимметричной системы fe = 0 k = 0 Данная система линейных алгебраических уравнений дает возможность определить все значения Ла, т. е. разложить несим-, метричную систему на т симметричных систем. Если система исходных комплексных величин образует на комплексной плоскости замкнутый многоугольник, то система нулевой последовательности должна отсутствовать, т, е. число систем симметричных составляющих уменьшается на единицу и становится равным m - 1. Для иллюстрации отмеченных положений можно разложить несимметричную систему, состоящую из токов /д, /в и /с, на симметричные составляющие. Заданная система является трехфазной, поэтому должно быть три симметричных системы в форме составляющих - системы прямой, обратной и нулевой последовательностей. Первую обозначают индексом 1, вторую - индексом 2, третью - индексом 0. Исходные уравнения имеют следующий вид: /л = Лл + + Дл. == Лв + Дв + об, (10.3) Для системы прямой последовательности (рис. 10.34, а) б1-2я/3; iiA = ahB = a4tc. (10.4) Для системы обратной последовательности (рис.. 10.34, б) б2 = 4я/3; hAaHBahc. (10.5) Для системы нулевой последовательности (рис. 10.34, в) 6о = 0; /од = /ов=/ос = /о. (10.6) Система токов нулевой последовательности симметрична только, условно, так как такая система является неуравновешенной: Да +/ов +/ос = З/о- Из уравнений (10.1)-ь(10.6) находят три линейных алгебраических уравнений с тррмя неизвестными /хд, Да и /оА = /о: А-Ла+Ла+Д; 1в = а1гА + а12А + 1о; - - ic=.aiiA + a42A + h. Совместное решение этой системы дает следующие формулы для определения симметричных составляющих: кА = 0А + а1в + аЧсЩ; А = {1А + аЧв + а1с)/3; 4= (А + /в + /с)/3. . . Если исходная система векторов образует замкнутый треугольник, то /а + /в+7с = 0, т. е. система нулевой последовательности отсутствует: 0 = 0. Поскольку в четырехпроводной трехфазной цепи ток в нулевом проводе равен сумме токов в проводах фаз на том же участке цепи (иногда этот ток замыкается через землю): /iv = /A +4 + 4. то при отсутствии других электрическихсвязей между соответствующими частями цепи Ij = 3lo, т. е. в нулевом проводе будет утроенный ток нулевой последовательности. Разложение на симметричные составляющие возможно для всех величин, входящих в многофазную систему:, токов, э. д. с, напряжений, сопротивлений, проводимостей и т. д.- При записи значений симметричных составляющих индекс фазы обычно опускают. Только при определении соответствующих значений величин одновременно для всех фаз или для разных фаз появляется необходимость в записи индексов, указывающих фазы. 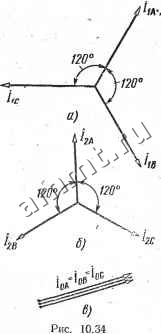 11 п/р. Ионкина, т. 1
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |