
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи индуктивностью Leo = /Соо- Сопротивление реализуется параллельно соединенными индуктивностью L,- и емкостью С/. Действительно, проводимость где Сг=1/2/Сг; Li = 2KM Таким образом, выражению (19.1) соответствует LC-схема двухполюсника, приведенная на рис. 19.1, а. 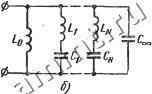 Рис. 19.1 Проводимость LC-двухполюсника удовлетворяет таким же условиям реализации, как и сопротивление. Поэтому разложение функции К(р) аналогично (19.1): Ксор. (19.5) где вычеты определяются по формулам (19.2)-f-(19.4), Слагаемое Ко/р реализуется индуктивностью Lo=l Co. слагаемое /СооР - емкостью Соо-Km Проводимость 2KiP реализуется последовательно соединенными индуктивностью Ц и емкостью Ci, так как Yi - 2Ki Р = L,p + 2/Сгр гце Li=l/2Ki; Ci~2Kif(iu- Схема двухполюсника, соответствующая выражению (19.5), приведена на рис. 19.1 б. Схемы двухполюсника на рис. 19.1, G, б называют каноническими схемами Фо-стера. По заданной входной функции также можно построить другие схемы двухполюсников. На рис. 19.2 показан двухполюсник цепочечной структуры. Входное сопротивление такого двухполюсника выражается непрерывной дробью: Z(p) = Zi- F4 + ... Если сопротивление Z(p) имеет полюс при р = оо, то нетрудно выделить слагаемое вида pLx или, говоря условно, выделить полюс при р = оо: . Z{p)pUZ{p). Функция 1/Z (р) также имеет полюс при р = оо: .l/Z(p) = pC2 + r(p). Последовательное выделение полюсов при р = оо приводит к непрерывной дроби Z(p) = pLi +-Ц-, (19.6) рС, + ... которой соответствует двухполюсник на рис. 19.3, а. Непрерьшная дробь (19.6) практически получается путем последовательного деления числителя функции Z(p) на знаменатель, начиная со слагаемых высших степеней. Сначала вычисляют значение индуктивности Li и остаток от деления Z (р); затем числитель функции, обратной остатку [функции 1/Z(p)], делят на знаменатель и находят значение емкости Сг и новый остаток от деления Y {р) и т. д., 0-!ZD-H Рис. 19.2 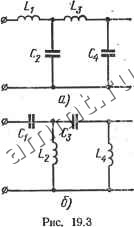 Если функция Z(p) имеет полюс при р = 0, то можно выделить слагаемое вида 1/pCi или, говоря условно, выделить полюо при р = 0: Z{p) = -+Z(p). Функция HZ{р) также имеет полюс при р = 0: l/Z(p) = (lW + r(p). БЗО . Последовательное выделение полюсов при р = 0 приводит к непрерывной дроби +... которой соответствует схема на рис. 19.3, б. Непрерьшная дробь (19.7) получается путем деления числителей функции Z (р) и соответствующих остатков на знаменатели, начиная со слагаемых низших степеней. Схемы на рис. 19.3, а и б называют каноническими схемами Кауэ-ра. Если проводимость Y (р) имеет полюс при р==оо или 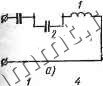
2/2S S/4- Рис. 19.4 Рис. 19.5 Z(p) = p = 0, TO разложение в непрерывную дробь функции У(р) имеет вид, аналогичный правой части выражений (19.6) и (19.7), только Lk заменяется на Ck и наоборот. пример 19.1. Построить канонические схемы Фостера и Кауэра, если входное сопротивление двухполюсника р4+4ра+з (р2 + 1)(ра + 3) р? + 2р р(р2-1-2) Решение. При разложении Z (р) на элементарные дроби в соответствии е формулами (19.1) (19.4) получим (Р)=+2(р2 + 2У+Р- На рий. 19.4, а приведена первая каноническая схема Фостера, на которой значения индуктивностей и емкостей указаны соответственно в генри (Г) и фарадах (Ф). Разложение проводимости У (p) = l/Z(p) на элементарные дроби имеет вид Y{p)- 2(p2-f 1) 2(р2 + 3) Чему соответствует вторая каноническая схема Фостера (рис. 19.4, б).
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |