Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 [ 131 ] 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

- Зависимость характеристического сопротивления 1сг от со/юо показана на рис. 14.13, с. В полосе пропускания это сопротивление является активным, при этом в области, непосредственно примыкающей к резонансной частоте, оно мало изменяется с частотой и равно У L,/Ci. В области низких частот сопротивление ZcT имеет емкостной, а при частотах, больших 2, - индуктивный характер. Зависимость характеристического сопротивления Zen изображена на рис. 14.13,6, при этом, так же как сопротивление ZcT, в зоне прозрачности оно является активным.

Пользуясь полученными соотношениями, можно найти расчетные формулы для определения параметров Li, Ci, Lz, Сз полосового фильтра. Прежде всего задаемся сопротивлением нагрузки /?2, равным характеристическому сопротивлению фильтра .при частоте о, т. е. Rz = VL2/C1. Затем по известной разности частот устанавливается следующая связь:

откуда .

, Индуктивность Z,2 находим из выражения о = тЛ = OitOa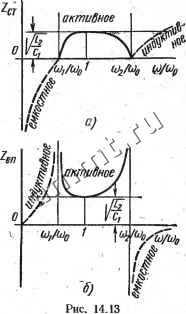

/?2(ю2-<0,)

Так как Л- = ;?2, то

Заграждающие (режекторные) фильтры. Если в схемах полосовых фильтров типа k поменять местами параллельно и последовательно соединенные ветви из емкостей и индуктивностей, то Б полученных схемах фильтров (рис. 14.14, с, б) при частоте <Оо можно получить разрьш продольных сопротивлений Z и короткое

замыкание поперечных проводимостей Y. Для этого необходимо выполнить условия

В этом случае

1 щи 1 /юСз

/соС,+-

/(0L2

Границы полосы пропускания находим из уравнений

= 0; -YZ

Из первого уравнения

- = 4.

со = 0; со = ос,

(14.26)

из второго уравнения

Ю2=СОо(/ п2+1+ П),\

где п= -L / ~-. Из полученных выражений следует, что фильтр пропускает частоты от О до coj и от со до оо. Полоса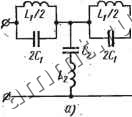

-0 0-

0 0-1---1-0

Рис. 14.14

задерживания расположена между частотами cog и щ, причем roo=<u2COi. Уравнение фазовой характеристики фильтра в полосе пропускания имеет следующий вид:

(14.27)

cos Ь = 1

Уравнение, определяющее затухание фильтра в полосе задерживания, записывается в виде

ChG=:

\щ со;

<14.28)

На рис. 14.15 в соответствии с (14.27) и (14.28) построены частотная [с(со/шо)] и фазовая [Ь(со/соо)] характеристики заграждающего фильтра.

Характеристические сопротивления для схем заграждающего фильтра на рис. 14.14, с, б определяются по формулам

1 .

(14.29)

На основании этих выражений, на рис. 14.16, с, б построены -зависимости Zct и Zen от со/соо.

Если принять сопротивление нагрузки равным характеристическому сопротивлению заграждающего фильтра при частоте соо, т. е. R2 = y L2/C1, то, аналогично полосовому фильтру, можно получить следующие формулы для определения параметров заграждающего фильтра:

С2.=

2 (Юз-Юг)

2(Юз-Ю2). зЮзЮз

27?2(Юз -Юг). Ю2Ш3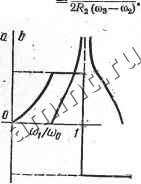

Рис 14. IS § 14.4. Фильтры типа т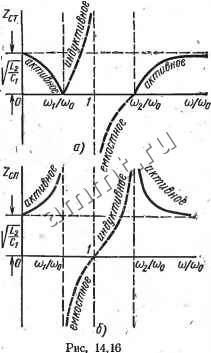

Одним из наиболее существенных недостатков фильтров типа k является зависимость характеристического сопротивления от частоты (см. рис. 14.8, 14.10, 14,13). Поэтому согласовать фильтр

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 [ 131 ] 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.