
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Уравнение (17.13) непосредственно следует из уравИенийк (17.4а), (17.8) и (17.9), а уравнение (17.14)-из уравнений (17.46), (17.10) и (17.11). § 17.2. Расчет напряжения прямой волны Пусть источник э. д. с. с напряжением о (О подключается к началу линии без потерь через пассивный четырехполюсник Я с сосредоточенными параметрами. Рассмотрим явления, происходящие в начале переходного процесса, когда после замыкания ключа (рис. 17.2) в линии возникает прямая волна, а обратная волна еще не появилась (Uo6n = 0). В этом случае, согласно уравнениям (17.12), (17.13) и (17.14), 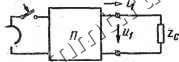 Рис. 17.2 Рис. 17.3 напряжение и ток в начале линии (л: = 0) совпадают с напряжением и током прямой волны, а также напряжением и током на выходе четырехполюсника: 1 (О = пр (, 0) = h (О = гЛр {t, 0) = гЛ (О- (17.15) Из этого соотношения следует, что эквивалентная схема для определения напряжения и тока в начале линии (до прихода обратной волны) состоит из пассивного четырехполюсника Я, к входу которого подключается источник э. д. с. с напряжением Ufsit), а к выходу - активное сопротивление, равное волновому сопротивлению линии Zc (рис. 17.3). Сопоставление уравнений (17.8) и (17.15) показывает, что уравнение прямой волны в начале линии совпадает с уравнением полного напряжения, а в остальных точках отличается от него fx \ только аргументом вместо Л. Следовательно, для получе- ния уравнения напряжения прямой волны необходимо в уравнении напряжения в начале линии заменить / на / --: np = l (17.16) По этому уравнению можно рассчитать напряжение прямой волны в любой момент времени />0 в точках линии, для которых xvt, по известному уравнению напряжения в начале линии. Пользуясь формулой (17.12), легко найти и уравнение тока -прямой волны. Пример 17.1. К началу воздушной линии длиной / = 120 км присоединен источник э. д. с. с напряжением Uo=Ua (1 -е ). где Uo = \OQO кВ; а =5000 ci. Построить график распределения напряжения прямой волны вдоль линии спустя 0,6 с после начала распространения волны. и р,кВ 1000 х.км 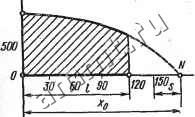  Рис. 17.4 0.2 0,4 Рис. 17.5 t.NC Решение. Исходя из того, что напряжение в начале линии совпадает с напряжением источника энергии, и учитывая общее правило (17.16), напряжение прямой волны t х\-\ t=0 i e-4-)L \. np = Kl 5-10 0,6. lO-s - J kb, Рис. 17.6 = 10001-e где t; = 3-105 km/c. График распределения напряжения прямой волны вдоль линии построен на рис. 17.4. Сравним график распределения напряжения вдоль линии в зависимости от координаты X с графиком изменения напряжения в начале линии в зависимости от времени t (рис. \Т1Ъ). Кривые напряжения на обоих графиках имеют одинаковую форму, что нетрудно увидеть, если предположить, что линия имеет большую длину, и продолжить график распределения напряжения до точки Xo - vt (см. рис. 17.4), до которой могла бы распространиться волна к рассматриваемому моменту времени t = 0,6 с. Аналогия графиков напряжения Mnp(-f) и i(0 носит более общий Xg=Vt Рис. 17.7 характер. При надлежащем выборе X масштабов для аргументов кривая распределения напряжения вдоль линии (в зависимости от координаты l, = vt~x) должна полностью совпадать с кривой зависимости напряжения в начале линии от времени t. Для этого достаточно выбрать масштаб для расстояний так, чтобы m - vmi, где щ~ Масштаб времени. Если линия присоединяется к источнику постоянной э. д. с. < = (/ (рис. 17.6, а), то напряжение в начале линии до момента включения (/<0) равно нулю, а после включения (/0) равно U (рис. 17.6, б). Поэтому распространяющаяся по линии волна имеет форму импульса бесконечной длины с прямоугольным фронтом (рис. 17.7). § 17.3. Ток и напряжение в конце линии Расчетные уравнения для напряжений и тока в конце линии могут быть получены из уравнений (17.12), справедливых для любой точки линии: Тогда согласно (17.13) и (17.14) I = inp -обр = ( np/2c) - ( o6p/Zc); Z£ = np - обр; = пр + обр-Почленное сложение последних двух уравнений дает В дальнейшем токи и напряжения в конце линии будут отмечаться индексом 2, а в начале линии - индексом 1 (рис. 17.8). Например, если последнее уравнение, справедливое для любой точки линии, должно быть использовано для конца линии, то его можно переписать следующим образом: Рис. 17.8 2ы2пр = 2 + гЛ, (17.17) где Ugnp - напряжение прямой волны в конце линии; tj -ток в конце линии; Wg -напряжение в конце линии. Уравнения (17.17) недостаточно для определения тока и напряжения, так как в него входят две неизвестные величины ( 2 и (г)- Дополнительное условие, связывающее неизвестные, зависит от нагрузки. Например, для активной нагрузки 2 = Па, (17.18) где г - сопротивление нагрузки. Расчетные уравнения для этого случая принимают вид гс+г (17.19) (17.20)
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||