Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 [ 107 ] 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

жений Ul, f/a) можно записать следующие уравнения: ei = i

2 = 2 = 21/1 +22/2 J

(11.1)

Zu = Uijii, Z21 = U2II1 - при /а = 0; Zz-UIh, Z2i-=Uill2 при /1 = 0

(при питании четырехполюсника со стороны выходных зажимов 2-2).

Форму записи уравнений (11-1) называют формой Z. В матричном виде эти уравнения можно представить как

(11.2)

(11.3)

		Z11Z12
		.2122,

Совместно решая уравнения (11-1), находим выражения для токов Л, /а:

. /i=Fiif/i+Fiaf/a;

/a = r2if/i+ra2f/2, где . -

22 . \Г 12

9.9. -

ZiiZ-Z12Z21

Г21 =

11 22-Z12Z21 - Z2I

Z11Z22 - Z12Z2I

Уравнения (11.3) можно получить непосредственно из схемы на рис. 11.1, пользуясь методом узловых потенциалов. При этом входные и взаимные проводимости определяют из следующих соотношений:

511 = и i/U i)u==o (входная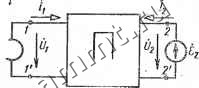

проводимость со стороны вход-НЫХ зажимов при закороченных выходных);

K22 = (/2/f2)t/,=o (входная

проводимость со стороны выход- Pjjj. jj j

НЫХ зажимов при закороченных -.

входных); - .

ii2 = (/i/2)ui=o (взаимная проводимость при закороченных . входных зажимах);.

i2i = (/2/i)t/5,=o (взаимная проводимость при закороченных выходных зажимах).

Форма Записи уравнений (11.3) носит название формы Y. Эти уравнения в матричном виде записывают аналогично (11.2):

(11.4)

		.KgiKaa,

Существуют еще четыре формы записи уравнений четырехполюсников, две из которых представляют интерес. С помощью одной из форм, называемой гибридной (смешанной) или формой Н, устанавливается связь между й, 1 с одной стороны и Л, с другой:

11 = -

(11.5)

		HiiHiz

7-, HlZ - 212/22;

fizl --rZgi/Zgg; /22= 1/22-

Матричная форма уравнений (11.5) записывается следующим образом:

(11.6)

Гибридную форму записи уравнений используют, например, для характеристики невзаимных цепей с электронными и полупроводниковыми приборами.

Для исследования режимов четырехполюсников при каскадном соединении следует иметь такую форму записи уравнений, при которой напряжение Ui и ток Д выражены через напряжение

Uz и ток Д. Для этого по теореме о компенсации э. д..с. 2 заменяем падением напряжения в сопротивлении Zg от тока /g,

направленного навстречу (о (рис. 11.2). При изменении положительного направления тока Д в уравнениях (11.1) изменится знак перед током /2: .

1 = 2иД - 212Д \ (И 7)

222- J

f/j - Z21/1 - Z,

В результате совместного решения уравнений (11.7) относительно Ul и II получаем:

f/i = f/2 + /2 = Л+ /2;

Ii = -U,+h = CU2 + Dh,

21 21

(11.8)

где Л = Zu/Z2i - безразмерная величина; В~ имеет

размерность сопротивления; C=l/Z2i имеет размерность проводимости; D == Z22/Z21 - безразмерная величина.

Форму записи уравнений (11.8) назьшают формой А*.

* Указанное наименование формы записи уравнений объясняется тем, что иногда коэффициенты .в уравнениях (11.8) обозначают буквой А, но с различными индексами, аналогично формам записи уравнений (11.1), (И-З) и (11.5).

Коэффициенты четырехполюсника Л, В, С и D срязаны между собой следующим соотношением:

Z21Z2

21

Так как для взаимных цепей Zia = Z2i, то

ЛС-ВС=1, Уравнения (11.8) в матричной форме имеют вид

		А В~

(11.9)

(11.10)

Если в схеме четырехполюсника (рис. 11.2) поменять местами источник э. д. с. и сопротивление приемника, т. е. к зажимам /-/ присоединить сопротивление Zi, а к зажимам 2-2 - источ-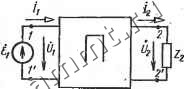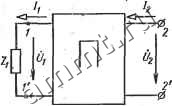

Рис. 11.2

Рис. 11.3

ник э. д. с. с напряжением U2 (рис. .11.3), изменив при этом положительные направления токов /] и на обратные, то уравнения (11.8) примут вид

UiAU2-~Bl2, \

-li=CU2~Dl2. ]

Из этих уравнений с учетом (11.9) находим

U2==DUi+Bii,\ l2CUi + Ah. ]

(11.11)

(11.12)

Из сравнения уравнений (11.8) и (11.12) следует, что при замене первичных зажимов вторичными (при обратном питании) коэффициенты Л и D меняются местами.

Четырехполюсник называют симметричным, если при замене первичных зажимов вторичными токи источника и приемника не изменяются. Уравнения симметричного четырехполюсника должны остаться неизменными при взаимной замене- первичных и вторичных зажимов. Поэтому Л==С и разметка первичных и вторичных зажимов для симметричного четырехполюсника не обязательна. Все четырехполюсники, не удовлетворяющие этому условию, называют несимметричными.

- -г ..

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 [ 107 ] 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.