Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [ 28 ] 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

т. е.

G(> = [R( )]-i; RC) = [G ]-!.

Формулы (4.3) и (4.4) представляют собой аналитические выражения закона Ома в матричной форме.

Система уравнений для токов и напряжений ветвей. Для цепи с. источниками постоянной э. д. с. и тока в установившемся режиме, по первому закону Кирхгофа,

А1() = 0 . (4.5а)

или

QI() = 0; (4.56)

по второму закону Кирхгофа,

Ви(> = 0. (4.6)

Уравнения (4.5а) или (4.56), (4.6) совместно с (4.3) или (4.4) полностью определяют режим цепи и позволяют решать задачи ее анализа.

Целесообразно несколько видоизменить уравнения, записываемые по законам Кирхгофа. Если обозначить столбцовую матрицу в сопротивлениях .(т. е. матрицу, в k-u строке которой записывается Iriy.

то из равенства (4.5а) следует

Ab = AJ(). (4.7)

Произведение AI, определяет матрицу, элементы которой равны алгебраическим суммам токов в сопротивлениях (т. е. токов /г), присоединенных к соответствующим узлам; при этом с положительным знаком записывают токи, направленные от узла, и наоборот. Произведение AJ ) дает матрицу, элементы которой равны алгебраическим суммам токов источников тока, присоединенных к соответствующим узлам; при этом с положительным знаком записьюают токи, направленные к узлу, и наоборот.

Таким образом, равенство (4.7) представляет собой матричную запись первого закона Кирхгофа в форме (1.13)-.

Аналогично формулируют уравнения для сечений:

QI,:QJC). (4.8)

Если обе части равенства (4.3) умножить слева на матрицу В и учесть равенство (4.6), то

BR()[lC) + J()j = Efe) . (4.9)

BR<)I, = BC). (4.10)

Произведение диагональной матрицы сопротивлений ветвей RC) на матрицу токов 1 дает вектор напряжений на сопротив-

лениях, т. е. вектор, элементы которого представляют собой произведения / fe/rj. Произведение матрицы. В на матрицу э. д. с. fC) определяет столбцовую матрицу, элементы которой равны алгебраической сумме э. д. с. контуров. Таким образом, уравнение (4.10) представляет собой матричную запись второго закона Кирхгофа в форме (1.17).

Расчет цепи с помощью уравнений Кирхгофа сводится ксовме-стному решению уравнений (4.7) или (4.8) и (4.10). Как правило, искомыми являются токи в сопротивлениях Irj при известных

к> Jk- Элементы матриц и J записывают с положительным или отрицательным знаком в зависимости от взаимной ориентации (fj и /г.

Вместо уравнений (4.7) или (4.8) и (4.10) можно составить дуальные уравнения для напряжений на сопротивлениях t/j,. Действительно, умножив обе части равенства (4.4) на матрицу А с учетом (4.5а), получаем

AG(>[UW-b<)] = AJ()

AG(>U, = AJ >,

(4.11) (4.12)

матрица напряжении на сопротивлениях.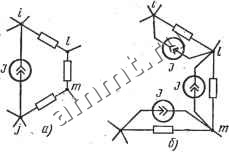

где U, = UW + W-Вместо уравнения (4.6) справедливо уравнение

BU, = BgW. (4.13)

Совместное . решение уравнений (4.12) и (4.13) позволяет вычислить все напряжения на сопротивлениях.

Следует подчеркнуть, что для относительно простых схем уравнения Кирхгофа могут быть составлены по сформулированным здесь правилам без записи матриц А, В и вычисления необходимых матричных произведений.

Особенности составления матричных уравнений при наличии ветвей с идеальными источниками. В схеме цепи могут быть ветви, содержащие только идеальные источники тока или э. д. с. Если уравнения, по законам Кирхгофа записываются непосредственно по схеме без применения равенств (4.10) или (4.12), то наличие ветвей с идеальными источниками не вносит никаких изменений.

Если при составлении уравнений по второму закону Кирхгофа применяют матричное равенство (4.10), то ветвям, содержащим только идеальные источники тока, соответствуют диагональ-

Рис. 4.3

ные элементы гй = со матрицы R(°. В этом случае схему необходимо преобразовать (рис. 4.3). Ветвь с источником тока J включена между узлами i и / (рис. 4.3, а). Включая в узлах / и т два противоположно направленных источника тока /, что не влияет на режим цепи, переходят к эквивалентной схеме на рис. 4.3, б. После подобного преобразования всех ветвей с идеальными , источниками тока записывают уравнение (4.10). Следует отметить, что такое преобразование уменьшает число ветвей и контуров схемы.

Если при составлении уравнений по первому закону Кирхгофа применяют матричное равенство (4.12), то ветвям, содержащим только идеальные источники э. д. с, соответствуют диагональные элементы gfc = oo матрицы G *. В таком случае схема должна быть преобразована (рис. 4.4). Ветвь с идеальным источником э. д. с. S включена между узлами i и / (рис. 4.4, а). В каждую из ветвей, соединенных с узлом / (или I), включают по одному дополнительному источнику э. д. с. S (рис. 4.4, б). Добавление одинаковых источников не изменяет режима схемы, так как точки k, I, т, п имеют одинаковый потенциал относительно узла и, . следовательно, их можно закоротить.

В ветви между узлами i и / два одинаковых источника направлены противоположно, поэтому напряжение на этой ветви равно нулю, т. е. такая ветвь эквивалентна короткозамкнутой ветви на рис. 4.4, в.

Таким образом, источник э. д. с. S (рис. 4.4, а) можно перевести за узел /, объединяя узлы i и / (рис. 4.4, в).

После подобного преобразования для всех ветвей с идеальными источниками э. д. с. записывакл уравнение (4.12). Данное преобразование уменьшает число ветвей и узлов схемы.

Недостатком метода расчета цепи по уравнениям Кирхгофа является большое число совместно решаемых уравнений и соответственно повышенные требования к точности промежуточных вычислений.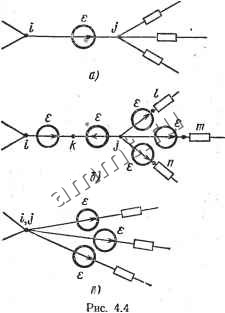

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 [ 28 ] 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.