
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Если в схеме на рис. 16.12, а параллельно ключу присоединено активное сопротивление г, которое после коммутации замыкается, то переходные напряжения и токи можно определить как сумму напряжений и токов в схеме до коммутации и в схеме на рис. 16.13, б. После коммутации в ветвь схемы (рис. 16.14, а) параллельно ключу может быть подключено дополнительное сопротивление г. Пере- Рис. 16.14 Рис. 16.15 ходные напряжения и токи в этом случае получают как сумму напряжений и токов в схеме до коммутации и в схеме на рис. 16.15, б, если последнюю дополнить сопротивлением/ , параллельным источнику тока 1к(0- Пример 16.5. Рассчитать ток ii(t) в цепи на рис. 16.16, ас помощью приведения цепи к нулевым начальным условиям. Параметры схемы: S=20 В; г1=/-а=/-а=10 Ом; /.=0,1 Г; С = 5.10- Ф. Рис. 16.16 Р е ш е н и е. До коммутации ток 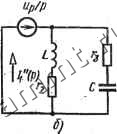 иапряжение на зажимах ключа = 1 А; /-1=10 в. Схема с нулевыми начальными условиями показана на рис. 16.16, б. Из этой схемы изображение тока Г<,у + + При переходе к оригиналам получим il (0=1- е-1в +е-200 Искомый ток i() = i + (T=2-е- +е-20о д. Следует отметить, что при подключении одного источника постоянной э. д. с. (тока) к пассивной цепи изображение искомого напряжени! (тока) имеет вид Р рВ{рГ При этом на основании теоремы разложения оригинал где pfc -полюСы, определяемые характеристическим уравнением Гармоническая функция е () = sin (coq + ip) представляет собой мнимую часть комплексной величины т- (т = тС-*), изображение которой равно т/(р -/fi>o). При подключении одного источника гармонического напряжения (тока) к пассивной цепи изображение искомого комплексного напряжения (тока) может быть записано следующим образом: Соответствующее мгновенное значение /(0 = lm L В (/СОо) Ad (Pk- /СОо) В (Pk) J (16.45) Формулы (16.44) и (16.45) называют формулами включения; первые слагаемые.в правой части этих формул определяют ycfa-новившееся значение напряжения (тока). § 16.6. Преобразование Фурье и спектральные характеристик! Преобразование Фурье и его основные свойства. Как уже отмечалось, прямое преобразование Лапласа существуетдля функций времени / (t), ограниченных условием / (Z) К Ме при Оо > О (/>0). Если функция f{t) удовлетворяет условию / () < Ме йри ао<0 (> 0), то эта функция абсолютно интегрируема. . Изображение по Лапласу F (р) абсолютно интегрируемом функции / (/) представляет собой аналитическую функцию переменной р в полуплоскости Re р > Од и в частности, на мнимой оси. Для такой функции в формулах прямого и обратного преобразования Лапласа можно принять р = /со. В результате F(/co)J/(/)e-/ d/; (16.46) со fit)-\pU<) d<>,. . (16.47) - со Формула (16.46) характеризует прямое преобразование Фурье, а формула (16.47) -обр а твое преобразование (интеграл) Фурье. Преобразования Фурье можно рассматривать как частный случай преобразований Лапласа при р = /содля абсолютно интегрируемых функций. Если абсолютно интегрируемая функция f {t) имеет изображение по Лапласу F(-p), то прямое преобразование Фурье этой функции F = F {р) ]р-/аз. В формуле (16.46) предполагается, что функция f{t) задана при >0. При <0 /(0 = 0. Если f{t)0 при /<0, то прямое преобразование Фурье имеет вид F{jw)= \ f{t)e-dt (16.48) и называется двусторонним*. Интеграл Фурье (16.47) определяет функцию f{t), равную или не равную нулю при <<0, если в подынтегральном выражении функция F{jw) соответствует формуле (16.46) или (16.48). В гл. 13 было рассмотрено разложение периодических функций f{t) в ряд Фурье. Такое разложение позволяет определить спектральный состав функции - амплитуды и начальные фазы ее гармонических составляющих. Интеграл Фурье представляет собой предельный случай ряда Фурье для непериоди<1еской функции. Переход от ряда к интегралу Фурье осуществляется следующим образом. Пусть f (t) - непериодическая функция, отличная от нуля в некотором конечном интервале времени А/= 4 -4- Выбирая произвольно период Г>-А/, можно образовать функцию /(0= Е f(t-kT). k=-со Эта функция является периодической и в интервале 4 < < 2 совпадает с функцией f{t) (рис. 16.17). Если Т-оо, то функция Jit) обращается в функцию f{t). W/:- * Аналогично можно определить и двустороннее преобразование Лапласа. . 465
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |