
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи ными характеристиками контура. Зависимости тока / и напряжений Ul, и с от частоты, называемые резонансными характеристиками, строят по соотношениям: и . <вс; ~аС~(оС 1аг2+(coL- 1/<в02 Резонансные характеристики изображены на рис. 7.29. 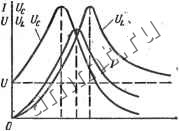
Шс ч Рис. 7.29 Рис. 7.30 Как видно из резонансных характеристик, ток достигает максимума при со = ио- Из уравнений df/i/do = О, d[7c/dtu = О получают выражения для частот coi и ©с. при которых напряжения Ul и Uc имеют максимум: tot = к 2Q2-1 При этом (Oi>(Oo, (Ос<(Оо; произведение (OiCOc = o- Если добротность Q < 1/1/2, то значения частот (О/, и (ос будут мнимыми, т. е. кривые Ul и Uc не имеют максимума. Выражение для тока можно преобразовать к следующему виду: где /о = [ / -ток при резонансе. 214 - На рис. 7.30 показаны зависимости /о от частоты для различных значений добротности. Область частот coisscotoa, в которой /о5s I/Y2, называют полосой пропускания контура (в этой области частот сопротивление контура мало). Из. приведенных кривых видно, что чем больше добротность, тем меньше полоса пропускания, т. е. выше избирательные свойства контура. Для частот ю, близких к юо, разность ю Ио ((О-(Ор) (ш+<йо) 2соД<в 2Д() где Дш = со - coq. На границах полосы пропускания 2Дсо/соо = = ±l/Q, следовательно, для контура с высокой добротностью СО2 - coi (Oq/Q. Из выражения, определяюш.его границы полосы пропускания, \Щ со/ следует, что граничные частоты щ и (О2 удовлетворяют соотношению C0iC02=C0. Иногда резонансные кривые строят в функции величин, называемых расстройками контура [х/г - обобщенная расстройка; Дев = со - соо - абсолютная расстройка; (со/соо) - (соо/со) - относительная расстройка]. Зная зависимости /, Ul, Uc от частоты со, можно строить зависимости /, Ul, Uc от расстроек. Резонанс токов. Резонансом токов назван режим цепи на рис. 6.28, при котором частота источника тока со = соо= l/lAIC. Если со = соо, то реактивная проводимость b = bL - bc = 0. Поэтому резонанс токов можно определить как режим цепи, при котором ее входная реактивная проводимость равна нулю. Частотные характеристики U (со), h{<ii), /с(<и) цепи на рис. 6.28 аналогичны соответственно частотным характеристикам /(со), (7с(со), f/i(co) цепи на рис, 6.22. На рис. 7.31 показана схе- Рис. 7.31 ма, содержащая две параллельно соединенные ветви. Частота сОр, при которой в цепи наступает резонанс токов, определяется из условия Ь = 0: b=bi+b2 =-~+ .i+7ipL)2-o- . После преобразований получаем rl + (mpL)\ 1+/-(ырС)2 . . I С откуда где (Oo=l/LC; р = /1/С.. Как видно из выражения для сОр, резонанс токов возможен при одновременном выполнении услрвий p>/ i, р> / г или p<ri, р<.Г2. Если эти условия не выполняются, то Мр - мнимое число. В случае, когда Гх = Г1, аЗр = (йо. При /1 = Г2 = р, (Ор = 0/0, т. е. резонанс токов наступает при любой частоте источника. При этом эквивалентное сопротивление контура 2x + Z2 (Р+/ £.) р-j вс). 2р+/ рсос). не зависит от частоты. Следовательно, ток 1 = 1] 1р в неразветвленной части схемы также не зависит от частоты. Если Гх и Гг - сопротивления, учитывающие потери реальных конденсатора и индуктивной катушки {гх - Гс, Н = Г1), то, как правило, рГх, рГг; при этом (Ор?= Шо. 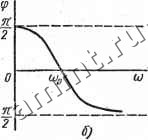 Рис. 7.32 В контуре без потерь (гх = Га == 0) ток J = bU = 0; токи II и /с равны по величине и противоп(1ложны по фазе. На рис. 7.32, а, б построены соответственно частотные характеристики fee Ь (м), i Ь (со) I и ф (со) = arctg (b/g) контура с потерями, дуального последовательному контуру гЬС. Эквивалентное сопротивление контура с потерями Z1+Z2 гх+г+Нч+х r+jx где хх = ~1/(йС; х&Ь; гГхЛ-г; хХх+х. В результате простых преобразований Zr, + jx где . - --Лй - При резонансе Xsp - O- Для контуров с высокой добротностью сОр СОо и д; - 1/соо£, 0; сопротивления Zx l/ajC; г% coL.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||||||||||||||||