
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи метричные фильтры имеют Т-образные (рис. 14.6, а) и П-образные (рис. 14.6, б) схемы. Коэффициент А- для этих схем имеет одинако- 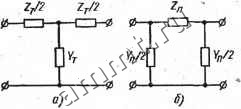 Рис. 14.6 , вое выражение, которое, например, для схемы на рис. 14.6,.а находим с по1\ощью топологической формулы, учитывая, что /2=0: 2 2 1 nWk откуда Л = 1 (14.5) Аналогичным способом получаем выражение для того же коэффициента для схемы на рис. 14.6, б: Л = 1 (14.6) Из выражений (14.5) и (14.6) следует, что коэффициент А не может принимать мнимых значений (проводимости Уп, Уг и сопротивления Zn, Zy -мнимые числа), поэтому уравнение Л =ch(a-l-/6) = chacos&-i-/shasin& распадается на два: - . sh а sin 6 = 0; chacosb = Л = 1 + (14.7) (14.8) Эти уравнения имеют два решения. Первое решение определяется условием, при котором sh а = О, и, следовательно, й = о, что соответствует полосе пропускания сигналов или, как иногда ее называют, зоне прозрачности. При этом cho!=l и из уравнения (14.8) с08б = Л = 14--2-. (14.9) Ползенное уравнение показывает, что знаки мнимых величин Y и Z должны быть одинаковыми: если, одна из них имеет индук- тивный характер, то другая величина должна быть емкостной . Диапазон частот, удовлетворяющих уравнению (14.9), определяется соотношением -11 + ~1. поэтому частоты, являющиеся граничными для полосы пропускания, могут быть найдены из равенств -TZ = 0;.-KZ = 4. - (14.10) Первое равенство определяет частоту, при которой закорачиваются продольные сопротивления Z и размыкаются поперечные, проводимости У четырехполюсника, - приемник оказывается как бы непосредственно присоединенным к источнику. Второе равенство определяет частоты, при которых каждая половина четырехполюсника, составленная из половины продольного сопротивления н половины поперечной проводимости, находится в режиме резонанса напряжений: Z/2-f 2/F = 0, / откуда . KZ-f4 = 0. Характеристическое сопротивление схем зависит от частоты, так как, согласно формуле (14.4), связано с коэффициентами четырехполюсника. Для Т-образной сХемы , ZoT = VBiC = V\A-m; для П-образной схемы . Zen = УШ = УВ1{А~\), Выразив сопротивления Zct и Zcm четырехполюсника через его коэффициенты, учитьшая при этом (14.5) и (14.6), можно получить: Z. -/S=/? - (14.12, Из последних выражений видно, что в полосе пропускания, для которой, согласно (14.10), 0 -ZK4, характеристическое сопротивление является чисто активным, причем с изменением частоты оно меняется в пределах от О до УЦУ для Т-образной схемы и от yZlY до оо для П-образной схемы. Это означает, что фильтр не может иметь одинаковый коэффициент передачи для всех частот полосы пропускания, если сопротивление приемника не изменяется. -Если, в частности, отношение ZIY фильтра не зависит от частоты и является вещественным числом, то в выражениях (14.11) и (14.12) от частоты зависит только произведение ZY. Экстремальное значение произведения и, следовательно, экстремальное значение Zc определяется из условия (ZK)=KZ + Zr = 0.3 Но так как Z/F не зависит от частоты, то / Z\ YZ-ZY \Y) ~ откуда YZ = ZY и, следовательно, 2KZ = 2rZ==0 или Z = 0, F = 0. При этом экстремальное значение Zc (максимальное для Т-образной и минимальное для П-образной схем) оказывается одинаковым для обеих схем и равным Y/Y = k, где k - вещественное число, не зависящее от частоты. Сопротивление приемника выбирают равным этой величине, поскольку вблизи своего экстремального значения характеристическое сопротивление Zc медленно меняетсяС изменением частоты. В полосе пропускания изменяется и коэффициент фазы Ь, знак которого можно определить с помощью соотношений B/Zc = shg = sh{a+jb) = CZc, откуда (при й = 0) / sin 6 = CZc == YtZct или / sin 6 = B/Zc = Zn/Zcn-Таким образом, знак коэффициента фазы b равен знаку продольного сопротивления Z (поперечной проводимости К). Второе решение уравнений (14.7) и (14.8) определяется условием sin 6 = 0. Так как cha 1, то cosfe = -1, а уравнение (14.8) записывается в виде сЪа~А = -[1-ьЩ. (14.13) В этом случае коэффициент затухания афО, что соответствует полосе задерживания сигналов (зоне затухания). Границы этой полосы определяются из соотношения l-fl+ ;оо. откуда -KZ = 4; -FZ = oo. Последнее равенство приводит в схеме фильтра к разрыву продольных сопротивлений и к короткому замыканию поперечных проводимостей. Поскольку в этом случае Л-1 =cho!-10, то согласно формулам (14.11) и (14.12) характеристическое сопротивление в зоне затухания становится чисто мнимым и имеет разные знаки для П- и для Т-образных схем. Знак реактивного характеристического сопротивления можно определить, исходя из следующих рассуждений:
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |