Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [ 24 ] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

можно лишь непрерывное изменение напряжения Ыс соответствующее непрерывному изменению энергии в электрическом поле конденсатора.

Энергетические соотношения в цепи на рис. 3.7 полностью аналогичны соотношениям, полученным для цепи на рис. 3.5.

Пусть конденсатор, заряженный до напряжения <f, в момент = 0 подключают к сопротивлению г (рис. 3.9). После

Рис. 3.8

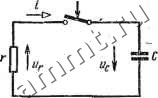Рис. 3.9

замыкания клющ конденсатор разряжается. Для этой цепи спса-ведлибо уравнение

+ с = 0.

(3.19)

откуда

По условию, Uc (0) = S, следовательно.

Ток в цепи

dur S -L

Кривые изменения напряжения с н тока i при разряде конденсатора показаны на рис. 3.10. Вся энергия,-запасенная в емкости, рассеивается в сопротивлении г.

Параллельная цепь. Для цепи на рис. 3.11 справедливо уравнение (при разомкнутом ключе)

Учитывая, что

получают дифференциальное уравнение

du dt

du , .

(3.20)

Если момент времени = 0 соответствует моменту включения источника постоянного тока и Uc (0) = 0. (конденсатор не заряжен), l.u С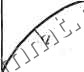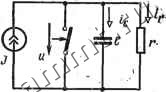

Рис. 3.10

Рис. 3.11

то по аналогии с решением (3.5) уравнения (3.1) записьшают решение уравнения (3.20):

Ток в емкости

ток в сопротивлении

c = cf=Je-5 t, = = y(l-e -I

(3.21) (3.22)

(3.23)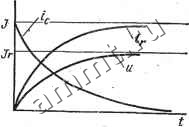

Графики зависимостей (3.21)-г-(3.23) показаны на рис. 3.12.

При установившемся режиме емкость эквивалентна разомкнутой ветви и весь ток источника замыкается через сопротивление г. Энергетические соотношения в цепи на рис. 3.11 аналогичны энергетическим соотношениям в цепи на рис. 3.1.

При равенстве численных значений соответствующих параметров цепи на рис. 3.1 и

3.11 являются дуальными. Такое утверждение справедливо и для цепей на рис. 3.5 н 3.7.

§ 3.4. Цепи с сопротквленкевл г, индуктивиостью L и ешостьЕО С

Последовательная цепь. Для последовательно соединенных сопротивления г, индуктивности L и емкости С, подключаемых к источнику постоянной э. д. с. (рис. 3.13), справедливо уравне-

Рис. 3.12

ние (при замкнутом ключе)

1 + г + С = <,

l + +iS = - (3.24)

Дифференцируя по времени обе части равенства (3.24), легко получить линейное дифференциальное уравнение второго порядка

g-b2a-bcoi = 0, . (3.25)

где 2а = гIL, (o = ;.

. Уравнение (3.25) -однородное; это означает, что ток в данной цепи имеет только свободную составляющую,. Действительно, при установившемся режиме, когда ток инапряжения на всех элементах постоянны, ветвь с емкостью эквивалентна разомкнутой ветви.

Общее решение линейного однородного дифференциального уравнения и-го порядка определяется корнями харак-- теристического уравнения, которое по-

лучается из дифференциального уравнения заменой производной -го порядка (й = 0, 1, п) множителем р*. Для уравнения (3.25) характеристическое уравнение имеет вид

p2 + 2ap-f = 0. (3.26)

. Корни характеристического уравнения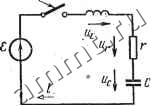

Px,2=-a±Vo?-l. (3.27)

Возможны три случая.

1-й случай. Если а>щ, то корни pi и Рз вещественны и различны. При этом общее решетке уравнения (3.25) записывают в виде суммы двух экспонент:

i = = AiePi + AePi, (3.28)

где AiH Az - постоянные интегрирования, определяемые из начальных условий.

Пусть в момент включения источника = 0 ток i(0) = 0 и напряжение с(0) = 0. Тогда из равенства (3.28)

i-f 2 = 0. (3.29)

Из уравнения (3.24) находят значение производной в начальный момент времени, учитывая, что г(О) -О, Uc {0) = 0:

dt t-o~ L

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [ 24 ] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.