
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи i)i = f>2e WP и /i = /2e e/P. то Л = f/i/i cos = f e cos # = Следовательно, к. п. д. линии 11 = 2/ = 6 °. Полученные соотношения позволяют определить единицу измерения затухания мощности линии из выражения al=~ In Р/Р2. Единицей затухания мощности служит непер (Ни). Затухание равно 1. Нп, если а/=1 или Pi/P2 = e. Таким образом, при затухании в линии, равном 1 Нп, активная мощность в начале линии больше активной мощности в ее конце в е = 7,39 раза. Очень важной характеристикой. линии является ее входное сопротивление, равное отношению Ui/Ii в начале линии. На основании уравнений длинной линии в гиперболических функциях Uj U2 ch yl+Zj2 sh уг у Z+Zc th yt п9 Ой\ Ii ishY/ + 4chy Z.thyl + Z, Для разомкнутой линии (/2 = 0, Z2 = oo) f/ip (Jzchyl Zc При коротком замыкании. (6/2 = О, 22 = 0) Zs.. к = = tf = Zc th yt. (12.28) Следовательно, зная параметры линии и сопротивление Zg, можно найти входное сопротивление линии при любой нагрузке. Пользуясь выражениями для Zbx.p и Z, можно определить волновое сопротивление линии Z а также thyl и коэффициент распространения у. Умножая друг на друга левые и правые части выражений (10.27) и (10.28): Zbx. pZex. к - jjj yi Zc th yt = Zc, получаем ZcVZZZ. (12.29) Аналогично можно найти формулу для определения ihyt: th т = К2вх.к/2вх.р. (12.30) Полученные выражения совпадают с формулами (11.44), что и следовало ожидать, так как цепь с равномерно распределенными параметрами всегда можно заменить симметричной эквивалентной Т- или П-образной схемой с сосредоточенными параметрами. Сравнивая уравнения для симметричного четырехполюсника А: \ h = C02i-Dl2 12* 855 с уравнениями длинной линии Ui = U2chyl + Zchshyl; il = (O/Zc) sh V/ + /gch V/, определяем значения коэффициентов четырехполюсника: A=D = chyl; B = ZcShyl; C = -l-shyl. (12.31) , Условие . для симметричного четырехполюсника - ВС = 1 выполняется и для длинной линии . . ch2v/-sh2v/= 1. . (12.32) Пользуясь выражениями (12.31) и (12.32), находим: . Zя = 2la = Z,shY; Zi = 2a = 2 = A; (12.33) = = ет: 2; = 2J = Z=.fci)-.. (12.34) Таким образом, по известным параметрам линии с помоигью формул (12.33) и (12.34) можно определить параметры эквивалентных П- и Т-обр5зных схем. Пример 12.1. Для определения параметров телефонной линии длиной / == = 200 км измерены при угловой частоте со=5000 с сопротивления разомкнутой ZBx.p = 747e~ Ом и короткозамкнутой 2вх.к=516е ° Ом линии. По формулам (12.29) и (12.30) найдены Zc=621e~° и у = (0,0046+/0,018) = = 0,00186е° . Определить первичные параметры линии: Гц, go, Cq и Lq. Решение. Для определения и Lq перемножим T = I{o+/ Lo)teo+/ Q на ZcY, т. е. YZc=ro+/coLo=(5,4+/10,21) Ом/км, откуда /-0=5,4 Ом/км, Lo== 10,21/5000 = 0,002 Г/км. Аналогичным путем найдем go и С : . - -=o + /wCo=(4,l 10-+/3. 10-6) 1/ом км, откуда go=4,l 10- См/км; Со = 0,006 .10-е ф/км. § 12.5. Линия без потерь В линиях передачи электрической энергии, применяемых в радиотехнике, телефонии и телеграфии, при достаточно высокой частоте можно с большой точностью пренебречь сопротивлением Го и проводимостью утечки go по сравнению соответственно с величинами coLo и (оСо- Поэтому во многих случаях такие линии рассматривают как линии без потерь энергии, что является идеализацией реальной линии. Для линии без потерь коэффициент распространения у = а + /Р = V (/-о + /fi)Lo) (go + / Со) = /со 1/ 1,;Со, е. а = 0; P = co1/LoCo. Волновое сопротивление такой линии При этом 8 = 0, tJ = co/p = I/I/LoCq, Я, = 2я/р. Следовательно, в линии без потерь коэффициент затухания равен нулю, а волновое сопротивление и фазовая скорость не зависят от частоты. Поэтому уравнения длинной линии в гиперболических функциях (12.-16) преобразуются в уравнения в тригонометрических функциях: I=hch(jx) + shiix) = hcosf,x + ismf,x. j Если. Ulh, 12 = h , то из этих уравнений легко получить выражения, определяющие мгновенные значения напряжения и тока: uUzmCOS fix siniiit-\-Zchm sin х sin co/-fy - Фг); г = sin pjc sin (со/ -f -5] -f Ism cos л: sin (са/ - фа). (12.36) Ha рис. 12.8, a, б изображены кривые распределения мгновенных значений напряжений и тока вдоль линии для / = 0 и t = T/6 на участке линии длиной % при ф2>0. Из уравнений (12.36) и этих кривых следует, что распределение напряжения и тока вдоль линии в каждый момент времени является синусоидальным. Если в конце линии включено комплексное сопротивление Z2 = =Г2-{-}х2, то входное сопротивление линии б з потерь == =---- j sin pZ + ZaCos j 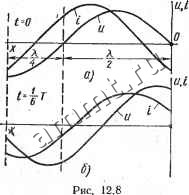 В уравнениях (12.35) ч-(1237) 2е = Ze = YLq/Co не имеет мнимой составляющей и по своему характ теру аналогично активному сопротивлению. Иначе говоря, отношение напряжения к току для прямой или обратной волн есть постоянная величина, не зависящая от частоты.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |