
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи 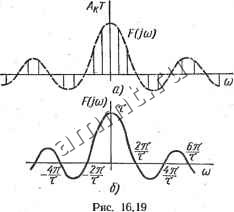 увеличивается, то число линий дискретного спектра возрастает, расстояние между ними уменьшаете; в пределе дискретный спектр переходит в сплошной. Амплитудная и фазовая спектральные характеристики прямоугольного импульса показаны соответственно на рис. 16.20, а, б; каждая перемена знака sin((0T/2) учитывается при изменении фазы на я. Если начало импульса совпадает с моментом времени == О, то амплитудная характеристика не изменяется а фазовая - дополняется слагаемым ci)t/2 *. При увеличении (уменьшении) длительности импульса расстояние между нулями функции F (со) уменьшается (увеличивается). Если амплитуда импульса равна 1/т, то при т->0 спектральная характеристика (M = limlsinf =1. . Импульс, имеющий длительность X и амплитуду 1/х в пределе при т->0, представляет собой дельта-функцию Ь {t). Следовательно, спектральная характеристика дельта-функции вещественна и равна единице для всех частот ->-оо<(о<оо. На основании теоремы запаздывания спектральная характеристика дельта-функции b{t - to) равна F ijw) = е-модуль этой характеристики F(co) = 1; аргумент ф(со) = - 0)0- Спектральные характеристики абсолютно интегрируемых функций, для которых найдено изображение по Лапласу, могут быть получены с помощью замены в изображении переменной р на /со. 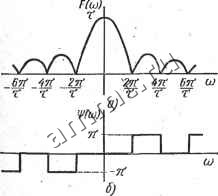 Рис. 16-20 * По теореме запаздывания, смещение импульса на т/2 (в сторону положительных значений t) приводит к умножению спектральной характеристики на е Пример 16.6. Построить амплитудную спектральную характеристику прямоугольного импульса с синусоидальным заполнением (рис. 16.21, а). Длительность импульса равна целому числу периодов. Решение. Заданная функция абсолютно интегрируема и описывается соотношениями f sin Юо<. 0<<<т 1 О, t>T. С помощью единичных функций заданную фyнкциюмoжнo представить в виде разности: f (0= sin СОо-1 (О -sin Юо (i-т) 1 (<-т). Следовательно, изображение функции / (О F (р) = Спектральная характеристика -(1-е-Р. Так как
модуль спектральной характеристики F( ) = 2 . сот -С02 пясо Амплитудная спектральная характеристика (со) приведена на рис. 16.21, б. Значение f (со) при со->сОо найдем с помощью правила Лопиталя: f (соо)=пл;/сОо. Нули функции F (СО) расположены в точках co = fecOo/ (* = 0, 1, 2,...). Если число периодов синусоиды п увеличивается, то значение F (сОо) возрастает, а расстояние между нулями функции уменьшается. Ряд важных функций времени (например, единичная и гармоническая функции) не являются абсолютно интегрируемыми. Спектральные характеристики таких функций не могут быть найдены непосредственно по формуле (16.46). Умножая функцию f{t) на экспоненту e~ во многих случаях удается найти спектральную характеристику произведения / {t) е . Если в этой характеристике принять (т = 0,то можно получить спектральную характеристику функции/). 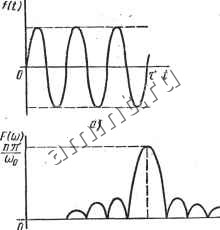 Рис. 16.21 f(t) С помощью рассмотренного приема в формулах для прямого преобразования Фурье производится переход от переменной /со к переменной р = а-\-]Ъ, т. е. вычисляется изображение по Лапласу функции f {t) с последующей заменой р на /со. Такой прием получения спектральной характеристики неинтегрируемой абсолютно функции нельзя считать корректным. Например, если единичную функцию 1 (t) умножить на экспоненту е , то спектральная характеристика этого произведения F (/со) = \ е-е- di = Рис. 16.22 Полагая о = 0, можно получить спектральную характеристику F(/co)= 1 со. Функция 1 с0 строго математически не является спектральной характеристикой единичной функции. Действительно, вычисляя обратное преобразование (16.47), получаем* CXI со cos со< sin со/ sin сог со dii) = L /со Y при при />0 Полученная функция \ {t), показанная на рис. 16.22, а, отличается от единичной функции 1 Ц). Ранее было показано, что дельта-функция b{t) имеет спектральную характеристику F(/co)=l. Если предположить, что для некоторой функции/() спектральная характеристика представляет собой дельта-функцию f (/со) = 6 (со), то на основании (16.47) /(0 = 4 5 6(co)e-dco=i 6(co)dco=l. -со -оо Таким образом, функции /(О = 1/2д при -оо<;оо соответствует спектральная характеристика в виде дельта-функции б (со). Функция t{t)=\ при -оо<<оо имеет спектральную характеристику 2я6 (со). Единичная функция 1 (t) может быть получена суммированием двух функций: функции на рис. 16.22, а, имеющей спектральную характеристику 1 со, и функции на рис. 16.22, б, спектральная характеристика которой л;б(со). Следовательно, спектральная харак- * Значение несобственного интеграла можно найти в математических справочниках.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||