
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи На рис. 13.1, б показаны постоянная составляющая, первая, вторая и четвертая гармоники, а также суммарная кривая i = = /о + h + h + Чу которая достаточно хорошо совпа- f(t) дает с заданной функцией. При разложении периодических функций на гармоники следует иметь в виду условия симметрии. Если функция нечетная, т. е. имеет симметрию относительно начала координат (рис. 13.2, a):f {t) = -f х X (-t),TO гармонический ряд должен состоять из синусоид с начальными фазами фй = 0. Если функция четная, т. е. имеет симметрию относительно оси ординат (рис. 13.2, б): f{t) = f (- t), то гармонический ряд должен состоять из синусоид с начальными фазами = зх/2. Если функция симметрична относительно оси абсцисс (рис. 13.2, е), т. е. tit) = -f{t + n), то гармонический ряд должен состоять из гармоник нечетного порядка: A = 2s-f 1, где S -целое число. Если функция одновременно симметрична как относительно оси ординат, так и относительно оси абсцисс, то гармонический ряд должен состоять только из синусоид нечетного порядка. § 13.2. Расчет установившихся процессов в линейных цепях Разложение периодических функций на гармоники позволяет рассматривать действительный несинусоидальный установившийся режим в линейных цепях как совокупность взаимно налагающихся синусоидальных режимов кратных частот. Например, если периодическая функция э.д. с, действующей в цепи, несинусоидальна, то можно считать, что одновременно действует целый ряд сину-соидальных э. д. с. кратных частот: е (О - 0+-7 2 - . Для каждой э.д.с. должны быть известны частотаJfeo) (номер гармоники) и комплексное значение э. д. с. Sk- Если цепь линейна, 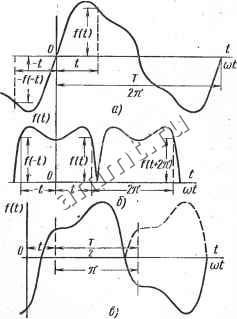 Рис. 13.2 то действие каждой э.д.с. можно рассматривать отдельно. При этом для каждой гармоники э. д. с. цепь следует представить в виде эквивалентной схемы - схемы замещения с соответствующими параметрами. Эквивалентные схемы, составленные для каждой из кратных частот, получаются при этом взаимно независимыми. В каждой схеме токи и напряжения имеют ту же частоту, что и все активные параметры - токи источников тока и э. д. с. Найденные при этом токи и напряжения определяют частичный рабочий режим цепи. Результирующие токи и напряжения для какого-либо участка цепи могут быть, определены путем суммирования всех гармоник по принципу наложения. Для каждого частичного синусоидального режима справедливы законы электрического состояния цепей: для узло для контуров . / Поэтому для расчета цепей применимы методы контурных токов, узловых потенциалов, преобразования цепей и т. д. Таким образом, расчет несинусоидальных режимов для линейных цепей сводится к расчету ряда синусоидальных режимов кратных частот и суммированию гармоник. В случае последовательной rLC-цепи для k-й гармоники тока. в комплексной форме справедливы следующие выражения: / , Ok Ok ; Uk Uk При этом для k = Q полное сопротивление Z(0) = oo, так как наличие конденсатора приводит к размыканию цепи при постоянном токе. § 13.3. Оообенности несинусоидальных режимов Сопротивления отдельных ветвей любой цепи различны для .разных частот. Прежде всего это относится к реактивным сопротивлениям и проводимостям, так как реактивное сопротивление ветви с. постоянной индуктивностью L Xki.=-k&L, а реактивная проводимость ветви с постоянной емкостью С bkc = koyC. 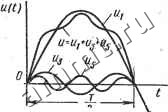 L(t) Для ветви, обладающей значительным индуктивным сопротиг влением на основной частоте (по сравнению с активным сопротивлением), относительная величина каждой высшей гармоники напряжения больше, чем у тока. Наоборот, для ветви, обладаю-, щей большой емкостной проводимостью на основной частоте (по сравнению с активной проводимостью), относительная величина каждой высшей гармоники тока больше, чем у напряжения. Для пояснения отмеченных положений следует рассмотреть простейшие примеры. Пусть напряжение, приложенное к индуктивной катушке, несинусоидально. При этом с помощью гармонического анализа установлено, что если амплитуда основной гармоники напряжения составляет 100%, то амплитуда третьей гармоники-15%, амплитуда пятой гармоники - 10%. Последующие гармоники имеют меньшие значения и не принимаются во внимание. При определении состава гармоник тока активным сопротивлением можно пренебречь. Для определения составляющих гармоник тока ток основной гармоники можно принять за 100%. Тогда амплитуда третьей гармоники тока составляет 15:3 = 5%, амплитуда пятой гармоники -10:5 = 2%. Таким образом, форма кривой тока оказывается ближе к синусоиде, чем форма кривой напряжения. Иначе говоря, индуктивность как бы сглаживает кривую тока, приближая ее к синусоидальной форме. Если принять напряжение на емкости имеющим такую же форму, как на катушке, то можно показать, что кривая тока в емкости искажена сильнее, чем кривая напряжения. Действительно, пусть ток основной гармоники составляет 100%. Тогда амплитуда третьей гармоники тока составляет 15-3 = 45%, амплитуда пятой гармоники-10-3 = 30%. На рис. 13.3, g, б построены кривые напряжения и тока в емкости за одну половину периода при указанных соотношениях в амплитудах. Начальные фазы у всех составляющих напряжения приняты равными нулю, а у каждой гармоники тока начальная фаза равна зх/2 (каждая составляющая тока опережает по фазе соответствующую гармонику напряжения на угол зх/2). Из сравнения кривых напряжения и тока следует, что форма кривой тока в ветви с конденсатором отличается от синусоидальной; форма же кривой напряжения на
Рис. 13.3
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||