
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи планарной схемы для вычисления передаточных функций с помощью контурного определителя и его алгебраических дополнений применима топологическая формула (8.15), если предварительно перейти к дуальной схеме. -г- \ I I Рис. 8.20 Пример 8.9,. Вычислить проводимость YxlJUt схемы на рис. 8.20, я. Решение. На рис. 8.20, б изображена схема, дуальная исходной. Проводимость Yai = Zai = U/lf дуальной схемы. Согласно формуле (8.15), -si- дЗ YAYf + Y! + Yf) + YiY -йГ Определитель Д дуальной схемы найдем с помощью разложения по путям менщу узлами l**-З**; А= 2 niAt=YtYi{yi + Yi + Yi) + YiYiYi+ +YiYiYi+YiYi{Yi-YYi+Yi). Если проводимости ветвей дуальной схемы заменить сопротивлениями ветвей исходной схемы, то Ze(Z3-bZ4-bZ5)-fZ4Z5 Га--л- Д = Z3Z4 (Z2-bZB-bZe)-f Z4Z6Z2-bZeZ5Z3-bZeZ2 (Z3-fZ4-f Zb). § 8.6. Применение сигнальных (направленных) графов к анализу электрических цепей Как уже отмечалось, линейная электрическая цепь характеризуется различными системами линейных уравнений. Эти уравнения могут быть наглядно отображены в виде сигнального (направленного) графа. Применение сигнальных графов к анализу электрических цепей позволяет существенно уменьшить объем вычислений по сравнению с непосредственным разложением определителя и его алгебраических дополнений. Кроме того, сигнальный граф дает наглядную картину причинно-следственных свя- зей между параметрами схемы и ее напряжениями и токами; с помощью графа определяют влияние различных параметров схемы на передаточные функции. Далее рассматриваются основные определения, преобразования и свойства сигнальных графов на примере графов, отображающих узловые уравнения цепи *. Сигнальный граф, его преобразование и передача. Сигнальным графом называют направленный граф, находящийся в однозначном соответствии с системой линейных уравнений. Пусть дана система п линейных уравнений (индекс у для краткости опускается) уцф!-f у12ф2-f . + 1 фп =?= Л; к21ф1 + у22ф2 + . + угпфп = Л; ущф! + п2ф2 + ...+ УппФп = Jn. где 1 имеет размерность проводимости, %,=-Yi, аФп. систему (8.25) можно привести к следующему виду: Фх=siiti-f 212ф2-f -.-Ь з1лф +Л; Фг = %1ф1 + ЗагФг + . + 22 Ф + Л; (8.25) Полагая Ф = 1+ 2 2ф2 +...+ ппФп + Jn. (8.26) Уравнения (8.26) называют уравнениями в форме причина-следствие, так как в них каждая зависимая переменная ф; выражена как функция всех зависимых и независимых переменных. Сигнальный граф строится по уравнениям (8.26), для чего каждой завиеимой (ф,-) и каждой независимой (jl) переменным ставится в соответствие узел графа. Если коэффициент фО, то узлы Фг и ф,- соединяют ветвью, которая направляется от узла ф/ к узлу фг и которой ставится в соответствие коэффициент 3/,у, называемый передачей ветви. Узлы фг и У, соединяют ветвью, направленной к узлу ф/ и имеющей единичную передачу. Например, системе трех уравнений ф! = 211ф1%2ф2%зФз + Л; ф2 = 22191 + 22292 -f %зФз -f Л; Фз = 2з1ф1 + зд2-Ь 2ззФз + л * Все результаты имеют общий характер и непосредственно применимы к графам, соответствующим любой системе линейных уравнений. 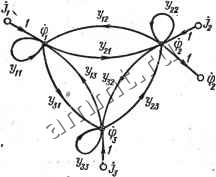 Рис 8.21 соответствует сигнальный, граф на рис. 8.21. Ветви, которые начинаются и заканчиваются в одном и том же узле ф/, называют петлями и имеют передачи, равные Ун. Если задан сигнальный граф, то можно записать систему уравнений, отображаемую графом. Уравнение, соответствующее узлу Фг, получается приравниванием переменной фг и суммы произведений передач всех ветвей, направленных к узлу щ, на переменные узлов, в которых эти ветви начинаются. Узел сигнального графа, к которому присоединены только исходящие ветви, называют истоком (узлом источника). Так, граф на рис. 8.21 имеет три узла (истока): /i, Л. Л- зел графа, к которому направлены все примыкающие ветви, называют стоком (узлом стока). Узлы графа с входящими и выходящими ветвями будем называть промежуточными. На рис. 8.21 промежуточным узлом является любой из узлов фх, фг. Фз- Промежуточный узел легко преобразовать в- сток, добавляя ветвь с единичной передачей, направленной из этого узла, и один узел (сток). Например, на рис. 8.21 узел фг преобразован в сток. Систему уравнений (8.26) можно решить методом исключения переменных. Исключению переменной фг соответствует основное преобразование графа - исключение промежуточного узла. Наиболее просто - исключается узел ф, в котором нет петли (3j,ft = 0). Так, если 2 ==0, то уравнение для п-го узла имеет, вид Фп = ЗшФ! + ЗпзФг +... + -1Ф -1 + Л. Подставляя выражение для ф в другие уравнения, получаем Фг = (2й + УщУпх) Ф1 + {1г + Vna) Ф2 + + + -1 + Ф -1 + Л + 3г Л. Таким образом, после исключения п-го узла ветвь, соединяющая узлы фг и фу и направленная к фг, имеет передачу УиУцЛ-УщУп, (i, У=1. 2. .... п-1). (8.27) Ветвь, соединяющая узлы фг и jt, не меняется, а между узлами Фг и У добавляется ветвь с передачей У{ . На рис. 8.22, а показан граф, являющийся частным случаем графа на рис. 8.21 при 333 = 0. Исключение переменной фз приводит к графу на рис. 8.22, б, передачи ветвей которого найдены по сформулированным правилам.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |