Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [ 127 ] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ГЛАВА 14

ЭЛЕМЕНТЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ

§ 14.1. Ооновные понятия и определения

Электрическим фильтром называют четырехполюсник предназначенный для выделения (пропускания) сигналов определенной (заданной) частоты.

Существуют различные способы классификации фильтров. В зависимости от пропускаемого спектра частот фильтры подразделяют на четыре основных вида:

1) (Шльтры нижних частот (низкочастотные) - ФНЧ, пропускающие сигналы в диапазоне частот от coi = о до cog (рис. 14.1, а);

2) фильтры верхних частот (высокочастотные) - ФВЧ, пропускающие сигналы в диапазоне частот от (Oi до со2 = оо(рис. 14.1,6);

3) полосовые (полосно-пропускающие) ПФ, пропускающие сигналы в диапазоне частот от coi до cog (рис.. 14.1, в)Г

м и,

(jLl2 U)

и>1 OJg (О

Рис. 14.1

4) заграждающие или режекторные (полосно-задерживающие) ЗФ, пропускающие сигналы в диапазоне частот от О до coi и от ©2 до оо (рис. 14.1, г).

В зависимости от типов элементов, из которых составлены фильтры, их делят на: . . ,

. а) реактивные, состоящие из элементов L и С; -б) пьезоэлектрические, состоящие главным образом из кварцевых пластин;

в) безындукционные пассивные, состоящие из элементов г и С; г) активные гС-фильтры и др.

Очень часто фильтры классифицируют по способу соединения элементов: Г-,Т-,П-образные, мостовые и др. По виду частотных характеристик фильтры подразделяют на фильтры типа k и т.

Каждый фильтр должен удовлетворять определенным требованиям, которые проще всего установить применительно к идеальному низкочастотному фильтру.

. На рис., 14.2 фильтр условно, изображен в виде четырехполюсника с напряжением на входе Ui и сопротивлением нагрузки Z ЧРи напряжении на выходных зажимах 0. Пусть фильтр пропускает сигналы низкой частоты от 0)1 = 0 до 0 = 0)2. Комплексный

13 п/р. Ионкнна, т. I

коэффициент передачи напряжения

К Ц(о) = i/jUi = U/iAU + Bh) = ZJ{AZ + В), (14.1)

где А, В, Zh - параметры, зависящие от частоты.

Комплексный коэффициент передачи можно представить в виде

/С(/со) = /С(со)е>Ч(), (14.2)

где /С (со) - амплитудно-частотная характеристика (АЧХ); Ф(со) - фазо-частотная характеристика (ФЧХ). В полосе пропускания для идеального фильтра справедливо равенство f/i = t/2, т. е. К (со) =< = 1. При этом сигнал сложной формы не должен искажаться.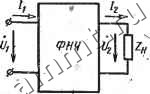

(р(со)

Рис. 14.2

Рис. 14.3

:со2,

Если напряжение на входе 1=2 ьт sin (кщ1 + и) для ncoi =

ft=i

то сигнал не искажается, при /С (со) = 1 и Ф (со) = - тсо, т. е. при линейной фазочастотной характеристике. Действительно, сдвиг фаз -й гармоники равен -хкщ, что эквивалентно сдвигу во времени -т:каУ1/кщ = - т. Иначе говоря, каждая

гармоника, проходя через фильтр, запаздывает на одно и то же время т, поэтому форма сигнала не меняется. На рис. 14.3,0!, б даны амплитудно-частотная и фазочастот-ная характеристики фильтра. Для идеального фильтра вне полосы пропускания сигналов /<(со)==0 и форма фазочастотной характеристики может быть любой.

При согласованной нагрузке комплексный коэффициент передачи напряжения

К (/со) = = e-s = e-e-JK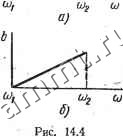

В полосе пропускания -коэффициент затухания а = 0, а коэффициент фазы b изменяется по линейному закону (рис. 14.4, а, б). Если в полосе пропускания К (со) зависит от частоты, а ФЧХ не ли-,нейна, то возникают амплитудные и фазовые искажения. На рис. 14.5, а показана кривая изменения мгновенных значений напря-

жения на входных зажимах фильтра Ui от времени, определяемая следующим выражением:

1 = sin a>t-\- Y sin Зсо/.

Пусть на выходных зажимах напряжение вследствие влияния параметров четырехполюсника определяется в одном случае <рис. 14.5, б) так:

Ыа = sin со/ 4- -g- sin Зсо/,

а в другом случае (рис. 14.5, в) - уравнением 2 = sino/--д-sin Зсо/.

Кривая U2 на рис. 14.5, б иллюстрирует амплитуднь1е искажения, вызванные изменением амплитуды третьей гармоники,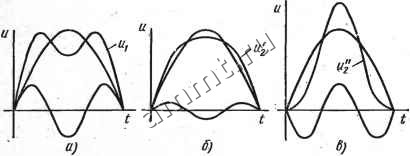

Рис. 14.5

а кривая Us на рис. 14.5, в -фазовые искажения, вызванные изменением фазы третьей гармоники.

§ 14.2. Симметричные реактивные фильтры

Как уже известно, симметричный четырехполюсник характеризуется следующими коэффициентами:

(14.3)

В свою очередь характеристическое сопротивление Zg и постоянная передачи g определяются через коэффициенты четырехполюсника по формулам

Zc=VbJC;

(14.4) (14.4а)

Пусть фильтр составлен из чисто реактивных элементов (индуктивных катушек и конденсаторов без потерь). Простейшие сим-

es = A-\-VBC или ch = y4.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [ 127 ] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.