
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Решение. Матрица контурных сопротивлений Z (P) = Г2 + Если приравнять к нулю определитель этой матрицы, то получим характеристическое уравнение вида (15.5): А-(р)=(.х+р1+)(..+)-(;=о. или после преобразования 1СГ2Р+(СГ1Г2+Ь)р+Гг+Г20. Узловой определитель ДУ (р) в цепях без взаимной индуктивности най- дем по топологической формуле. Так, записывая узловой определигель с помощью разложения по путям между узлами 2 (при замкнутом источнике (о) и приравнивая его к нулю, получим характеристическое уравнение вида (15.6): pL riV rl = 0. Для заданной схемы можно записать три уравнения вида (15.7), 1. Приравнивая нулю входное сопротивление относительно зажимов источника S, получим 2. Если Эамкнуть источник ё и разомкнуть ветвь с сопротивлением или емкостью С, то нетрудно получить уравнения, приравнивая нулю входные сопротивления относительно точек разрыва ветвей: Х.х2(р)Г2 + р±Ш§,0 ri+pL + {\lpC) (ri+pL)r = 0.. З.-Если приравнять к нулю проводимость между узлами /, 2, то получим характеристическое уравнение вида (15.8): После преобразования любого из уравнений и подстановки численных значений параметров найдем р2+200;?-f-20.108=0. Вычислим корни характеристического уравнения: Pi,2= -100 + /100. Порядок расчета переходных процессов классическим методом Токи и напряжения схемы при переходном процессе могут быть рассчитаны следующим образом. Анализируя схему до коммутации, необходимо найти значения. токов в индуктивностях и напряжений на емкостях: Il (0 ); Uc (0 ). Эти значения позволяют определить на основании законов коммутации независимые начальные условия, т. е. iz,(0+) =х,(0-) и с(0+) = мс(0..). в схеме после коммутации следует рассчитать принужденные составляющие искомых токов и напряжений. Далее для схемы после коммутации требуется составить характеристическое уравнение и определить его корни. Искомые величины следует представить как суммы свободных и принужденных составляющих и вычислить постояннее интегрирования. Начальные значения искомых величин и их производных, необходимые для вычисления постоянных интегрирования, находят с помощью независимых начальных условий и уравнений цепи. Рассмотренная методика расчета переходных процессов применима и к цепям, содержащим электронные лампы и транзисторы. Пример 15.2. Рассчитать напряжение а (<) на выходе лампового резонансного усилителя, эквивалентная схема которого приведена на рис. 15.3, при подключений источника гармонического, напряжения (<)=f/mi sin (<й<+ {)). Рейение. Нагрузкой резонансного усилителя счужит параллельный контур L-С-г. Параметры данного усилителя таковы, что характеристическое уравнение для этого контура 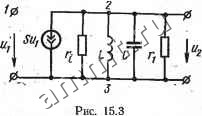 имеет комплексно-сопряженные корни. Для схемы на рис. 15.3 можно составить уравнение где r=rirtJ{ri-\-r{). После дифференцирования этого уравнения получим dt L~ dt у dt г Следовательно, характеристическое уравнение принимает вид Полученное уравнение эквивалентно уравнению вх(Р)=ч-рС-Ь = 0. JBx (р) - входная проводимость относительно узлов 2-S при Kj=0 и 1-0,т. е. при разомкнутом зависимом источнике тока. Таким образом, для заданной схемы можно воспользоваться соотношением (15.8). Если обозначить J (f)Jm sin (fi)<-bil)) = - Ski sin (ю+ф), to для определения напряжения tu (t) можно воспользоваться выражениями, полученными в § 6.7; aw. v Для цепей с электронными элементами и взаимной индукцией запись характеристического уравнения в виде (15.7) и (15.8) может быть затруднена, поэтому для составления характеристического уравнения целесообразно воспользоваться другими способами, например применить выражения (15.5) и (15.6). § 15.2. Переходные и импульсные характеристики цепей При анализе цепей во временной области часто применяют две специальные функции: единичную функцию и единичный импульс. Единичную функцию 1() определяют следующим образом (рис. 15.4, а),: при < 0; при > 0. (15.9) Функция 1(0 непрерывна всюду, кроме точки / = 0; значение функции 1 (О в точке разрыва можно считать неопределенным *. - ГШ т-г) 1 Рис. 15.4 Рис. 15.5 Аналогично можно Определить функцию 1( -т)(рис. 15.4,6). 0 при <т; 1 при t>x. (15.10) Умножение любой ограниченной функции f {t) на 1 (if -т) дает функцию ° Р < . (15.11) \f(t) при t>x. /(01(-т) = * Можно также считать значение функции в точке разрыва равным 7г или 1.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |