
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Если за положительное направление тока принять направление к узлу, то уравнения для сечении Sj и S3 совпадают с уравнениями для узлов. По второму закону Кирхгофа, 1 + з + 5=0 (контур /); 4 - 5- з+ 2=0 (контур ); 6 - з+ 2==0 (контур П1). § 2.3. ToncncrEJ4S3Kiis /{атрицы графа и их свсйства Уравнения по законам Кирхгофа для токов и напряжений могут быть записаны в матричной форме. Например, независимые уравнения для трех узлов графа на рис. 2.12 + h +4 = 0; -4 + 4 -эквивалентны матричному уравнению = 0; 4 = 0 0-1 0 10 1 -1 1 10 0 о L о 0-101-1 Аналогично в матричной форме можно записать уравнения для сечений и контуров. Левая часть таких уравнений представляет собой произведение матрицы коэффициентов на столбцовую матрицу переменных. В правой части уравнения записана столбцовая матрица, все элементы которой равны нулю. Матрицы коэффициентов уравнений Кирхгофа состоят только из элементов +1, -1 и 0. Значения этих элементов определяются только структурой графа (схемы) и могут быть найдены при рассмотрении графа (схемы). В соответствии с видом уравнений Кирхгофа различают три топологические матрицы: матрицу соединений (узловую) А, матрицу сечений Q и матрицу контуров В. Матрица соединений (узловая матрица) А - это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для узлов. Строки этой матрицы соответствуют узлам, столбцы - ветвям. Если элемент матрицы А обозначить через aij, т. е. А = [ау] (t -номер строки, / - номер столбца), то можно сформулировать следующее правило составления матрицы: ау=1, если ветвь./ соединена с узлом i и направлена от узла; ау=-I, если ветвь / соединена с узлом i и направлена к узлу; ау==0, если ветвь / не соединена с узлом i. Обычно число строк матрицы А равно числу независимых узлов, т. е. д = у-1. Если узловую матрицу записывают для всех у узлов, то ее обозначают A. Пример 2.2. Составить матрицы Ан, и А для графа на рис. 2.15. Решение. Матрица Ац, записанная Для всех 5 узлов, имеет вид Ан=, Вычеркивая любую строку, получают матрицу А. Если вычеркнуть строку, соответствующую узлу 5, то
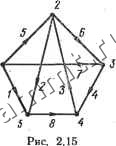 Сумма элементов каждого столбца матрицы Ли равна нулю, так как каждый столбец матрицы содержит только одну + 1 и одну -1, а остальные элементы столбца нулевые. В матрице А может отсутствовать одна строка матрицы Ац, соответствующая любому узлу. Если обозначить через столбцовую матрицу токов всех ветвей, то уравнение Ai(=) = 0 (2.5) будет представлять матричную запись первого закона Кирхгофа. С помощью матрицы А нетрудно выразить напряжения всех ветвей через потенциалы узлов. Для этого элементы k-й строки матрицы А следует умножить на фд, -потенциал k-ro узла, затем сложить элементы каждого столбца. В /-м столбце может быть +1 в k-й строке и -1 в t-й строке, если /-я ветвь присоединена между k-M и t-M узлами и направлена от k-ro узла. Тогда напряжение /-й ветви м,= Фй -ф/.
Таким образом, матрицы напряжений ветвей и узловых потенциалов связаны равенством и(=) = АЧ), (2.6) - соответственно столбцовые матрицы напряжений ветвей и узловых потенциалов, причем потенциал последнего узла фд.1 = фу = 0; А -транспонированная узловая матрица. Матрица сечений Q - это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Строки матрицы Q соответствуют сечениям, столбцы - ветвям. Элемент qij матрицы Q = [gij.] определяется следующим образом: qij=l, если ветвь / содержится в сечении и направлена согласно с направлением сечения (т, е. с направлением для замкнутой поверхности); qij =-1, если ветвь / содержится в сечении i и направлена противоположно направлению сечения; qij=0, если ветвь / не содержится в сечении L Если матрица Q составлена для главных сечений, то ее называют матрицей главных сечений. При этом за,положительное направление сечения обычно принимают направление ветви дерева данного сечения. Пример 2.3. Для графа на рис. 2.16 записать матрицу главных сечении. Решение. Выбранное дерево (ветви /-2-3-4) и сечения показаны на рис. 2.16. Номер сечения считаем совпадающим с номером ветви дерева. Матрица сечений 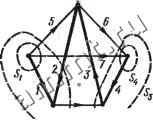 Рис. 2.16 Q = 2 3 12 3 4 10 0 0 0 10 0 О О 1 4 LO О О. 1 6 О О О -1 О -1 -1 -1 -1 8 О .-I -1 0J Число строк матрицы Q равно числу независимых сечений д. Матрица Q может быть получена с помощью линейной комбинации строк матрицы A. Так, в матрице Q (см. пример 2.3) строки 1 и 4 совпадают со строками I и 3 матрицы Ан (см. пример 2.2). Строку 2 матрицы Q получаем как сумму строк 1 и 5
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||