Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 [ 133 ] 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

типа m преобразуется в фильтр типа к. Для частот а)>.сосо сопротивления и имеют одинаковые знаки, поэтому для определения величины затухания в этом диапазоне следует воспользоваться выражением

4Z ,

(14.35)

вместо (14.34), так как последнее справедливо только для схемы с комплексньши значениями Z и Zm, имеющими разные знаки.

Выражения для характеристического сопротивления при различных значениях параметра m имеют разный вид. На рис. 14.24 изображены кривые изменения характеристического сопротивления Zcnm со стороны входных зажимов Г-образного фильтра (рис. 14.21, б) для различных значений т. Эти кривые построены по уравнению (14.12), в котором Z = Zirn и y=l/Z2m. При т = 0,6 величина характеристического сопротивления Zcnm в большей части полосы пропускания ближе к значению характеристического сопротивления фильтра, равного \L/C, чем при m = .l. Это означает, что режим работы фильтра при указанных параметрах в большей части полосы пропускания будет близок к режиму согла-

П7=0,31

Рис. 14.23

Рис. 14.24

Рис. 14.25

сованной нагрузки, если сопротивление нагрузки выбрано равным

Wc.

. Если в схеме Г-образного фильтра (см. рис. 14.21, ) принять Zvm - Z/m, то сопротивление Zim можно определить из уравнения Zcnm = Zcn, т. е.

Vz./yi+-VZxZ/f 1+§

откуда

~ tnZi t 2Z2m

(14.36)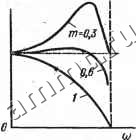

Рис. 14.26

Из полученного выражения следует, что если сопротивление поперечного звена принять равным 2Z2m = 2Z.Jm = 2/](отС, то продольная . проводимость, равная обратной величине продольного сопротивления должна состоять из двух параллельных ветвей с параметрами

2/j(>)Lm и /(оС. В результате по-

лучается Г-образный, так называемый параллельно-производный фильтр (рис. 14.25).

На рис. 14.26 построены графики изменения характеристического сопротивления ZcTm для различных значений т. Из этих графиков видно, что, так же как для характеристического сопротивления Zcnm (см. рис. 14.24), при тя 0,6 сопротивление Zcrm мало отличается от величины У L/C во всем диапазоне пропускаемых частот.

Недостатком фильтров типа т - является снижение затухания* при fi>,> fi>oo (для фильтров нижних частот и полосовых фильтров) и при е> < ©со (для фильтров верхних частот и полосовых фильтров).

§ 14.5. Безындукционные гС-фильтры

При построении реактивных LC-фильров наиболее громоздким и дорогим элементом является индуктивная катушка, особенно в фильтрах, работающих в диапазо- не низких частот. В таких схемах применяют индуктивные катушки с ферромагнитными сердечниками, как правило, имеющие очень большое число витков. Катушки с большим числом витков и громоздкими

сердечниками обладают низкой добротностью Qi = ()yoL/r, так как в них имеются потери не только в обмотках, но и в сердечниках. Таким образом, катушка не является идеальной индуктивностью,

40<f.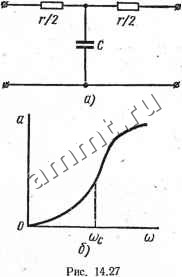

в результате основные характеристики фильтров с катушками, имеющими низкую добротность, ухудшаются.

В настоящее время широкое применение находят интегральные схемы, в которых возможна микроминиатюризация элементов г и С. При этом индуктивная катушка, применяемая на низких частотах, не поддается миниатюризации.

Следовательно, целесообразно построение фильтров без индуктивных катушек, т. е. лС-фильтров. Рассмотрим простейшие примеры построения таких фильтров.

Т-образный фильтр нижних частот. На рис. 14.27, а изображена схема Т-образного лС-фильтра. .

Для этой схемы при /2 = 0 справедливо уравнение

СЛ 2

Ох = О 2+/шс у 62 = (1 + /ft) у)=лО,

откуда

Л = [/1/£/2=1+/а)у. Для симметричного четырехполюсника

(14;37) (14.38)

Л = ch g = ch (й + jb) = ch а cos & -j- / sh a sin &.

Приравнивая правые части уравнений (14.37) и (14.38), получаем:

chacos6=l;

sh а sin & = -

(14.39).

(14.40)

При постоянном токе (а) = 0)

ch а cos & = 1 г / sh G sin & = 0.

Эти равенства имеют решение одновременно при а: = 0 и Ь = 0. Если (u>0, то sin&>0, так как при а>0 sha>0. В отличие от реактивных фильтров у гС-фильтров нет такой области частот, в.которой а = 0. Из уравнений (14.39) можно найти зависимость а qt ю. Для этого первое из уравнений (14.39) следует представить в виде

(l+sh2GHl-sin6)=l. Если в это выражение подставить значение sin&, найденное из второго уравнения (14.39), то можно получить биквадратное уравнение относительно sha:

откуда

sh*a-()%h.-(f = 0.

(orC

8 ~ 2 r При ы2/гС из выражения (14.41) находим

04.41)

sh а; = G я .]Ла)лС/2.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 [ 133 ] 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.