Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 [ 75 ] 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

Если к столбцу а прибавить столбцы а+1, а+2, то .матрица Ад преобразуется в матрицу

... а а+1 а-Ь2 а + 3 ... р-1 р..

/ + 1 /+з

				... 0
				... 0
				... 0
				... 0
				... 0

Таким образом, с помощью линейной комбинации столбцов матрицы Ад получена матрица Ад, у которой в столбце а имеется 1 в /-Й и -1 в k-K строках, причем все остальные элементы столбца а равны нулю.

Миноры матриц А у и А. рассматриваемой пары общих деревьев-г это определители матриц, полученных из матрицы Ад вычеркиванием /-й или k-u строк. Эти определители равны определителям матриц, полученных из матрицы Ад вычеркиванием /-й или ft-стррк, так как линейная комбинация столбцов не изменяет величины определителя.

Определитель матрицы Ад( /) или Ад получаемой при вычеркивании из матрицы Ад /-й или fe-й строк, может быть найден путе! разложения по элементам столбца а. Так, если из матрицы Ад вычеркнуть /-ю строку, то в столбце а останется лишь один ненулевой элемент -1, который находится в (fe-1)-й строке (при вычеркивании /-й строки номера последующих строк уменьшаются на единицу). Следовательно,

. detA;(( /) = (-l) + -M-l)£)=(-!) +*£),

где D - определитель матрицы, получаемой из матрицы Ад при вычеркивании /-й и к-й строк и столбца а.

Если из матрицы Ад вычеркнуть k-\o строку, то в столбце а останется лишь один элемент +1 в /-й строке. Поэтому

detA( ft)

Произведение

, detA;,( /)detAi( fe) =

= ( 1

поскольку D = ± 1 как определитель подматрицы узловой матрицы дерева. Таким образом, произведение пары миноров матриц А у и A,j, соответствующих общим деревьям двух схем, равно (-1)+*. Этот результат справедлив для любой нумерации узлов и ветвей и произвольной- ориентации ветвей.

Знаки соответствующих миноров матриц A /Y ;п Pi-k определяются знаками миноров матриц А / и А ;, поэтому определитель (8.5) имеет общий множитель (-1)+*. В р1азложении алгебраического дополнения А)==(-1)+*М/й присутствуют только положительные слагаемые, равные произведению проводимостей ветвей общих деревьев схемы с заземленными /-м и k-u узлами.

Рассмотрим алгебраическое дополнение Д(у) схемы на рис. 8.1, с.

Деревья графа, полученного при объединении узлов 1 я 4 (см. рис. 8.2), приведены на рис. 8.3, а. Если в исходной схеме объединить узлы 2 а 4, то результирующий граф (рис. 8.5, а)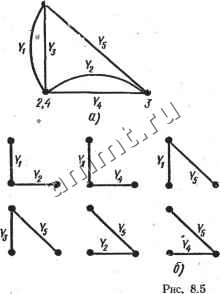

-Y Уз-П.

сумме четырех ветвей общих

будет иметь деревья, изображенные на рис. 8.5, б. У графов с заземленными узлами 1 я 2 имеются четыре общих дерева. Эти деревья содержат ветви Уг -Уз, Уг-Уб. В результате алгебраическое дополнение равно слагаемых, равных произведению проводимостей деревьев:

Ail = УгУз + ПУь + YsY, + УзП.

Топологическое правило для алгебраического дополнения можно видоизменить. Деревьям схемы, получаемой при заземлении /-го (fe-ro) узла, в исходной схеме соответствуют 2-деревья типа 7*2 (/,) {Tzik.y))- Общим деревьям двух схем соответствуют 2-деревья, у которых /-й и k-n узлы находятся в одной части, т. е. 2-деревья типа Тфу). Таким образом, алгебраическое дополнение Ду> равно сумме произведений проводимостей ветвей

всех 2-дереБьев типа Та уу В частности, для схемы на рис. 8.1, а алгебраическое дополнение А[у равно сумме произведений проводимостей ветвей 2-деревьев типа т2(Х2,4) (рис 8.6).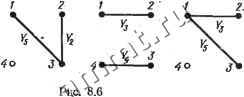

Если обозначить через Wjk,y сумму произведений проводимостей ветвей 2-деревьев типа Т2цн.в), то

% = fu,y. (8.6)

Формулу для симметричного алгебраического дополнения можно рассматривать как частный случай формулы (8.6):

Д1> = 1Г ,. (8.7)

Разность алгебраических дополнений. При вычислении передаточных функций В- соответствии с равенствами (7.53)1 (7.54) необходимо / г знать разность алгебраических дополнений вида Д1}>-А1Г- Но

Д,}>=1Гу., и Al> = r,ft, поэтому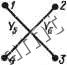

Рис. 8.7

Если 2-деревья типа T2(ii,y) содержат k-й узел в одной или в другой части схемы, то

где Wiik,y (Wi/, ft j,) -сумма произведений проводимостей ветвей 2-деревьев типа Та (ць, у) (Та (у. ку))- Аналогично,

где Wijk,y{Wik,jy) - cyuua произведений проводимостей ветвей 2-деревьев типа у) (Т (tk, jy))-

Таким образом, алгебраические дополнения Д} и Д имеют общие слагаемые, равные Wi/k, у. Если исключить общие слагаемые, то разность

lii-TW y-W ,jy. При заземлении узла I вместо у (см. рис. 7.36) разность

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 [ 75 ] 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.