
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Входная функция .Z{p) комплексной переменной р = 0-1-/0) имеет вид Z{p) = pT + = (a+jco)T+.=,VR(a, <o) + jX(a, со), где вещественная часть функции R{o, (>>) = <уТ +-, мнимая часть функции Х(с, (>>) = а>Т Вещественная и мнимая части аналитической функции Z(p) должны удовлетворять условиям Коши - Римана. Согласно одному из этих условий, dR(a, со) дХа, со) , да да Производная дЯ(с, (О) гр , дТ . cqz-g о dV да ~ да Т (о2+со2)2 o-j-co да следовательно, производная ах (о, со) = Г-Ь,. (18.18) где X(со) - реактивное сопротивление*. Правая часть равенства (18.18) пропорциональна сумме максимальных энергий магнитного и электрического полей, связанных с индуктивностями и емкостями в установившемся синусоидальном режиме (р = /со). Сумма энергий всегда положительна. ах (со) поэтому тивления Х(со >0, т. е. наклон графика реактивного сопро- положителен для всех частот. Условие положительности наклона справедливо и для реактивной проводимости, взятой с отрицательным знаком. Действительно, пусть при р = 0--/со функция F(p) = G(a, со)-/Б (0, со). Производная dV(p) dp dp Г 1 U(P)J 1 dZ (р) [Z (p)f dp Если p = i(x), TO F(/co)= -/Б(сй), где В (со) - реактивная проводимость. Производная dY(p) dB{6)) 1 dX(co)Q p /to dco [X(co)]2 d(o Из условия положительности наклона вытекают следующие свойства входного сопротивления Z (р) [входной проводимости Y (р)]: нули и полюсы сопротивления (проводимости) простые и чередуются, т. е. между канедой парой полюсов расположен нуль, а между каждой парой нулей -полюс. Пример зависимости Если р=/<о, то R(a, ю)=0, 2 (/ш) =/Х (ю). входного сопротивления X от частоты показан на рис. 18.7. Если между парой полюсов отсутствует нуль (или наоборот) или кратность полюса (нуля) больше единицы, то зависимость Х((о) будет иметь участки с отрицательным наклоном dX(co)/dcu<;0. Поскольку нули и полюсы входных функций чисто мнимые, в числителе и знаменателе функций можно выделить сомножители (Р - / ft) (Р + 1Щ) = р + (о. Такие сомножители при p = jiu принимают вещественное значение, однако Z(/co) и F (/о)- мнимые величины. Следовательно, в числителе или знаменателе входной функции кроме множителей вида р-1-(о должен быть мно-h / житель р, т. е. входная функ- ция цепи без потерь имеет полюс или нуль в начале координат (рис. 18.7 соответствует случаю, когда при р = 0 сопротивление имеет полюс). При р->оо входная функция также имеет полюс или нуль. Кратность этого полюса (нуля) равна единице, поэтому степени полиномов числителя и знаменателя отличаются на единицу (рис. 18.7 соответствует случаю, когда сопротивление имеет полюс при р -> оо, т. е. степень полинома числителя на единицу больше степени полинома знаменателя). В общем виде входное сопротивление цепи без потерь можно представить следующим образом: 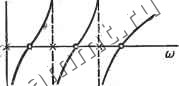 Рис. 18.7 7 (г.\ - (P + tf)(P + toi) -KP)-t\ p(; + o))(p2-fco) ... если в точке р = 0 функция имеет полюс, или 7 / ч Р(р +(о)(р +(о) - (18.19) (18.20) если в точке р = 0 функция имеет нуль. В формулах (18.19) и (18.20) О < (Oi < (02 <(0з < (О4 < Для входной проводимости цепи без потерь справедливы аналогичные выражения. Как видно из приведенных выражений, сопротивление (проводимость) представляет собой отношение четного полинома к нечетному или наоборот. Конечные нули и полюсы входных функций соответствуют резонансным частотам схемы. Нули и полюсы при р = 0 и р = оо соответствуют короткому замыканию или размыканию зажимов двухполюсника без потерь, который на очень низких или очень высоких частотах эквивалентен одной емкости или индуктивности. Вычеты в полюсах входных функций вещественны и положительны. Пусть сопротивление Z(p) имеет полюс при р = /(Оо и вычет в этом полюсе равен Ко- Тогда функцию сопротивления можно разложить в ряд Лорана: iP)=J=k + (Р -/ о)+а2 (р-/й>о) + .... Производная =-(. + 1 + 2аЛр-/со )+ .... . Если p = /fi)-*-/(Ooi то - р /о) rfco (со-wof Так как (ю - ©о) > О, вычет Ко в полюсе /юо - вещественная положительная величина. Вычет в сопряженном полюсе р = - /соо равен Ко * Свойство положительности вычета получено как следствие свойства положительности наклона кривой реактивного сопротивления. . . Необходимые условия реализации входного сопротивления (проводимости) цепи без потерь можно сформулировать следующим образом: 1) полюсы сопротивления (проводимости) простые и расположены на мнимой оси; 2) вычеты в полюсах вещественны и положительны. Фзшкции, удовлетворяющие этим условиям, называются реактансными. Свойства входных функций гС-, rL- и rIC-цепей. Если цепь содержит только активные сопротивления и емкости, то энергетическая функция Г = 0. На основании формулы (18.14) выражение для нулей сопротивления двухполюсника имеет вид p = - V/F. (18.21) Следовательно, нули и полюсы входных функций гС-цепи расположены на отрицательной вещественной полуоси. При р = о-1-/й) входное сопротивление такой цепи Z{p)=F+2 + i{-) = tio, <о) + !Х{а, со). Применяя одно из условий Коши -Римана, можно получить дЯ(а, со) дХ{с, со) га-о да . о=-<0- Учитывая, что Х{с, со) = 0 при со = 0, находим dR(a, (О) т. е. наклон графика функции Z{a) отрицателен для всех значений а. Нетрудно убедиться, что наклон графика Y (о) положителен: dF(a)/do->0. Если р->0, то гС-двухполюсник эквива- * В случае произвольной функции комплексной переменной р вычеты в сопряженных полюсах являются комплексно-сопряженными величинами.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |