
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи ковыми параметрами Li = L = L, Ci = C2 = C, = = г и, следовательно, Хх = Х2 = х (данная частотная характеристика аналогична частотной характеристике тока /g). Комплексная взаимная проводимость Y2i = lz/Ui = - ZM/(ZxZz-Zh) или (Zi = Z2==r+/X ZM=iXM) 21 - r2 x2+x, +{2гх= 1-{х/г)+(хм/г)+21 (xlr) Отношение a=xlr - обобщенная расстройка контуров (см. § 7.6). При резонансной частоте (Оо= l/]/ ZC, а = 0. При небольших отклонениях частоты (О от резонансной (небольших расстройках) J-(ао)(т+(Оо) / \ (оС/ \<Во шу (В(В( в областичастот, близких к отношение Хм/г = саМ/г = Kc(L/r Кс(Цг = KcQ. Модуль взаимной проводимости (е>. о). У21 = - KcQlr l/[l-c2+(KeQ)2]2+(2a)2 Наибольшее значение взаимной проводимости f/2imax= 1/2/ имеет место при полном или сложном резонансе [если контуры одинаковые, то (/2max)max= f/i/2/-]. Раздслив 1/21 на {/2шах, полу-чаем нормированную характеристику связанных контуров: 21 max (9.11) Величина отношения (9.11) при любой расстройке а зависит от произведения KjQ- В 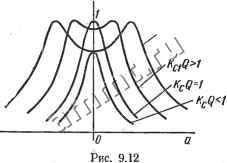 частности, при резонансе (а = 0) 2/CcQ aimax / -. (9.12) Отношение (9.12) принимает наибольшее значение, равное единице (при КД - = 1), т. е. в случае оптимальной связи. Если KcQ 1, то (f/2l/i/amax) < 1. Дифференцируя функцию (9.11) по а и приравнивая производную к нулю, вычисляем значения а, соответствующие максимумам функции (9.11): ai.2 = ±KOT-b функция имеет максимумы только при сильной связи, т. е. при /CcQ>l. Если KcQ<.U то Ci,2 -мнимые числа. Максимальные значения функции (9.11) равны единице. При сильной связи функция (9.11) имеет также минимум, определяемый выражением (9.12). При KcQ< 1 (слабая и оптимальная связь) функция (9.11) имеет только один максимум для а = 0. (Семейство зависимостей У21/Уитах для различных значений KcQ приведено на рис. 9.12. Связанные контуры при /CcQl позволяют получить более широкую полосу пропускания, чем у одиночного контура. Изменяя коэффициент связи, можно изменять форму частотной характеристики. § 9.3. Разветвленные цепи с взаимной индукцией Уравнения разветвленных цепей. Для разветвленной цепи с взаимной индукцией матрица комплексных сопротивлений ветвей
где элементы главной диагонали Zi, Zg, Z - комплексные сопротивления всех ветвей; элементы вне главной диагонали Zij - ~ Zji (i ФI) - комплексные сопротивления индуктивной связи t-й и /-Й ветвей. Сопротивление Zy == /ху = /соМ (Zy = - /ху = - /соМ), если ориентация t-й и /-й ветвей по отношению к одноименным зажимам одинакова (противоположна). Для ветвей, не имеющих индуктивной связи, Ziy = 0. Матрица проводимостей ветвей цепи с взаимной индукцией определяется как матрица, обратная матрице (9.13): Y( ) = [ZW]-i. (9.14) Зная матрицы Y) и Z, можно составить узловые уравнения, уравнения с напряжениями ветвей дерева и контурные уравнения (7.27), (7.28) и (7.29). Матрицы этих уравнений вычисляют, как и в цепи без взаимной индукции, по выражениям (7.30)-f-(7.35). Однако в отличие от цепей без индуктивных связей матрицы Z ) и Y) не являются диагональными. Матрицы Y(y), Z цепей с взаимной индукцией симметричны, так как симметричны матрицы Z) и Y т. е такие цепи удовлетворяют принципу взаимности. Во многих случаях не все ветви цепи имеют индуктивную связь, поэтому с помощью надлежащей нумерации ветвей матрице Z(> нетрудно придать квазидиагональную форму: где подматрицы Zu, Z22,..., Zm могут быть квадратными недиагональными или диагональными. Такое представление матрицы Z ) облегчает ее обращение, так как обратная матрица 11 Zmm- В качестве примера составления матричных уравнений можно рассмотреть схему на рис. 9.13, а, граф которой показан на -4=1-0- л 1 т Рис. 9.13 рис. 9.13, б. Матрица сопротивлений ветвей 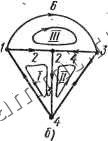
В этой матрице вьщелены три подматрицы, которые легко обращаются: Zr. = Z2.== Zi3 =
Yx У12 Y12 У2. Уз У34 Уз, У, A All = 12 - Zfa; A22 = Z3Z4 - Z34; YxZjAii, Y2 = ZxlAn; Y3=ZJA22, П = г.,/А22; У12 ~ - Z12/A11; У34 = - Z34/A22; Уь - i/Zbl Ye = 1/Ze.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |