
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Если вместо функции Zi(p) воспользоваться обратной функцией Yt(p)- 3(р + 1) то можно получить еще одну схему двухполюсника. Минимальное значение ReYi{j(i>) равно gi = ~ при ш = со. Функция имеет нуль при р = со. Обратная функция 3(р + 1) YiiP) 3 , 3 На рис. 19.7, б изображена вторая схема двухполюсника, реализующая заданную функцию Z(p). Следует отметить, что функция Zi (р) удовлетворяет необходимым требованиям для входных сопротивлений rL-двухполюсника. Реализации этой функции, показанные на рис; 19.7, а, б, соответствуют каноническим схемам Фостера. В общем случае ПВФ не может быть реализована рассмотренным выше простым методом; известны другие методы, позволяющие реализовать произвольную ПВФ. § 19.3. Реализация LC- и гС-четырехполюеников мостовой схемы Пусть задана передаточная функция четырехполюсника (взаимное сопротивление Zai(p)) при разомкнутых зажимах. Такая функция реализуется симметричной мостовой схемой, показанной на рис. 19.8., а (на рис. 19.8, б дано упрощенное обозначение мо- 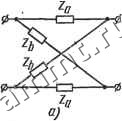 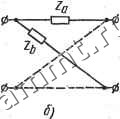 Рис. 19.8 стовой схемы). Так как четырехполюсник является симметричным, его входные сопротивления равны: ZuZgg. Условие вычетов (18.31) принимает вид/Си -/См 0. Можно потребовать, чтобы условие вычетов выполнялось со знаком равенства для всех полюсов. Вычет /Cii>0, а вычет /Cai может быть положительным или отрицательным, поэтому из условия вычетов Ки = \Кл\- Если вычеты функции Zia(p) в полюсах известны, то на основании равенства/Cu = /Ciaf, легко найти функцию Zu(p). Вычеты функ- aet...- ции (р) определяют при разложении этой функции на элшен-тарные дроби. Группируя слагаемые с положительными и отрицательными вычетами, можно записать Z2i(p) = ZS(p)-Zff(p). (19.16) где функции ZS(p) и Ziip) содержат слагаемые только с положительными вычетами. Полагая для каждого полюса Kii = \Kzi\, получаем выражение для входной функции: Zn(p) = ZS(p) + 2l(p). (19.17) По известным функциям Zii(p) и Ziip) можно найти сопротивления Zaip) и Zpip) мостовой схемы (рис. 19.8). Для мостовой схемы Zn==(Z + Z6)/2; Z2i = (Z6-Z )/2, откуда Z = Zii -Zax; Zi, = Zu+Zai. Если учесть выражения (19.16) и (19.17), то Z (P) = 2Z;,7>(P); . (19.18) Z,(P) = 2ZS(P). (19.19) Формулы (19.18) и (19.19) позволяют построить схему четырехполюсника. пример 19.4. Требуется реализовать функцию 1 = р (р2 +1) (р2+2) (р2+3) - Решение. Разложение функции Zl (р) на элементарные дроби имеет вид 7 ( Р . Р Р .. . iiW-Qp 2(ра+1) 2(р2+2) 6(р2+3) Следовательно, гй(р)=ё На основании выражений (19.18) и (19.19) ~ Р~2(р+1) + б(рН-З)- a(p)=T5+ rJ, 2б(р)=; p+l 3 (р2+3) Зр р2+2 Функции Za (р) и Zft (р) реализуются как входные сопротивления £С-двух-полюсников. На рис. 19.9 приведень! схема мостового четырехполюсника и параметры ее элементов. Пример I9.S. Реализовать функцию 7 м (р-1)(р-2)(р-3) **~(Р + 1)(Р+2)(Р+3)- Решение. Функция поэтому 7 r, 12 , 60 60 Z (P)=- + -+l, fiO 12 60 функции Za (р) Ц Zb (р) реализуются как входные сопротивления гС-двуя-полюсников; в результате получаем схему на рис. 19.10. / 7/5 f/24 tmo  3 ф--- Рис. 19.9 Рис. 19.10 Следует отметить, что каждому полюсу функции Z (р), расположенному-в левой полуплоскости, соответствует нуль, расположенный симметрично в правой полуплоскости. Амплитудно-частотная характеристика Zgi Ою) в таком случае не зависит от частоты. С помощью симметричного мостового четырехполюсника аналогично предыдущему реализуется функция (р). § 19.4. Реализация LC~ и гС-четырехполюсннков цепочечной охемы Четырехполюсники цепочечной схемы, как уже отмечалось, на-xj)mT широкое применение и могут быть построены по различным передаточным функциям, например, Zif (р), Yif (р). Пусть задана функция LC-четырехполюсника, нагруженного на активное сопротивление (см. рис. 18.10): < (р) = Л(р)/Б(р). (19.20) Если сопротивление нагрузки нормировано r-lOu, то для функции Fjf (р) справедливо выражение (18.39). Представляя полином В (р), равный сумме четной [т (р)] и нечетной [п (р)] частей, можно записать FaXp) А{р) (iq 2П 1 + П2(Р) т(р) + п(рУ . Полином А (р) может быть четным или нечетным. Если А (р) - Чётный полином, то выражение (19.21) приводится к виду 521 (Р) Aip)/n(p) откуда 1 + У22(р) 1 + Н(р)/п(р)1 (19.22) -У,г{р) = А{р)/п{р); (19.23) У2{р)т(р)/п(р). (19.24) Если Л (р)- нечетный полином, то выражение (19.21) следует представить в виде Yn (Р) y + Y(p) А(р)1т(р) l + [n{p)lm(j})l (19.25)
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |