Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 [ 29 ] 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

§ 4.2. Применение узловых уравнений

Узловые уравнения. Число совместно решаемых уравнений можно уменьшить, если в качестве независимых переменных принять потенциалы узлов. Знание потенциалов позволяет найти все токи в схеме.

Уравнения с узловыми потенциалами (узловые уравнения) вытекают из первого закона Кирхгофа; их число равно числу независимых уравнений, составляемых для узлов, т. е. у-1.

Выражение (4.11) перепишем в следующем виде:

Принимая потенциал одного из узлов равным нулю (а именно потенциал того узла, для которого отсутствует строка в матрице А), напряжения на ветвях определяем через узловые потенциалы (см. гл. 2):

U(>-av (4.14)

Таким образом, получаются уравнения вида AG<)A> = А JC) - AGCf С),

(4.15)

которые назьшают узловыми уравнениями в матричной форме.

Если обозначить

G(y = AGC)A; (4.16)

J(y)==AJ(B) AGC>)i( ),

то узловые уравнения запишутся более кратко:

(4.17) (4.18)

Матрицу G> называют матрицей узловых проводимостей, матрицу J<y -матрицей узловых токов. В развернутой форме уравнение (4.18) имеет вид

(4.19)

gllgl2 gl, 5-1		Ф1		-J(y)
gilgii gz,y-i
- gy-l. lgy-2, 2- gy-l, y-1 -		-Фу-1-

В качестве примера можно составить узловые уравнения для цепи на рис. 4.5, а.

Данная схема имеет 3 узла и 4 ветви. Граф схемы показан на рис. 4.5, б; ориентация ветвей выбрана произвольно. Узел 3 принимаем за базисный (фз = 0).

Узловая матрица

-1 0 1 Г

О -1 О -1

диагональная матрица проводимостей ветвей

Tmgk=l/rk; fe=l, 2, 3, 4.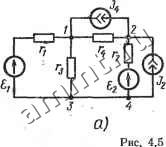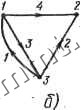

Матрица узловых проводимостей

-1 О 1 1 0-10-1

-I 0i

0 -1

1 -1

- gi 0 gs gi

L 0 -go -g,j

L -4

-1 0

0 -1

1 -1

Матрица токов источников тока ветвей JW = [0 -J О JJ; матрица э. д. с. источников э. д. с.

2 О Of.

Матрица узловых токов

J(y) = AJ ) - АОСШС) = А [J ) - G( О -gii

Г-1 0 1 1 0-10-1

gi + gs + ga -g4

0 -0

л -0 Таким образом, узловые уравнения имеют вид

h-\-g

g\x gn
	ф2

11=1+3+4; 12 = 21=-g*; §22й+&;

jm = J, + g,Sx; /у) = /2-Л+Я22.

Анализ результатов рассмотренного примера позволяет сделать ряд важных общих выводов:

1. В матрице узловых проводимостей на главной диагонали записывают суммы проводимостей ветвей, присоединенных к соответствующему узлу, с положительным знаком. Диагональные элементы матрицы называют собственными узловыми проводимостями.

2. Элемент gij матрицы узловых проводимостей (t Ф /) равен сумме проводимостей ветвей, присоединенных между узлами i и у, взятой с отрицательным знаком. Внедиагональные элементы матрицы называют общими узловыми проводимостями.

3. Матрица Gyi симметрична, т. е. gij - gji и 0(у = [С<]\

4. Элемент У матрицы узловых токов равен алгебраической сумме токов источников тока, присоединенных к j-му узлу, включая токи источников тока, эквивалентные источникам э. д. с. При этом с положительным (отрицательным) знаком записывают токи, направленные к узлу (от узла).

5. Знаки элементов всех матриц не зависят от ориентации ветвей графа.

Следовательно, узловые уравнения можно составить при непосредственном рассмотрении схемы.

Если в схеме имеются ветви с идеальными источниками э. д. с, то для записи уравнения (4.15) используют преобразование, показанное на рис. 4.4. Такое преобразование целесообразно и при непосредственном составлении узловых уравнений. Наличие в схеме ветвей с идеальными источниками тока не требует преобразования схемы: в матрице G! ветвям с идеальными источниками тока соответствуют проводимости gk = 0. Для уменьшения числа столбцов матрицы А возможно преобразование, показанное на рис. 4.3.

Пример 4.2. Рассчитать токи в схеме на рис, 4.6 методом узловых потенциалов. Параметры схемы: г1=Г2=/-з=2 Ом; 4=5=6 = 6 Ом; =(- = = 6 В; 7з=9 А.

Решение. Между узлами / и 5 включен идеальный источник э. д. с. ё ,. Переместив этот источник через узел /, получим схему на рис. 4.7, в которой

#j=,=6 В; й5=Й 2Н-7=12 В.

Пусть потенциал <ра=0. Тогда для схемы на рис. 4.7 справедливы узловые уравнения:

rSi+g2+gs -g3 -e-i 1ГФ11 Г~ з-gi<i -М

-& -& £2+ЁЪ +

Зф1-фз-ф4==-36; -Зф1ч:Ч-5ф4=36; -Зф1+5фз-ф4==Д4.

	-ф1-
	-ф4-

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 [ 29 ] 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.