Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [ 17 ] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

матрицы А , умноженных на -1; строка 3 матрицы Q равна сумме строк 3 и 4 матрицы Aj,.

Закон Кирхгофа для сечений в матричной форме записывают следующим образом:

Qi(=) = 0. (2.7)

Если матрицу напряжений ветвей дерева обозначить через и*), то

и(в) = дтц(д) (2.8)

т. е. напряжение любой ветви схемы определяют через напряжения ветвей дерева.

Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разделена на две подматрицы:

Q = [l F],

где 1-единичная подматрица порядка у-1, столбцы которой соответствуют ветвям дерева; F - подматрица, столбцы которой соответствуют ветвям связи (см. пример 2.3). 7

Матрица контуров (контурная матрица соединения ветвей) В - это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки матрицы В .соответствуют контурам, столбцы - ветвям.

Элемент bij матрицы В = [Ьу] определяется следующим образом:

bif = 1, если ветвь / содержится в контуре i и направление ветви совпадает с направлением обхода контура;

bij==-1, если ветвь / содержится в контуре i и направление ветви противоположно направлению обхода контура;

bij = 0, если ветвь / не содержится в контуре L

Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура.

Пример 2.4. Для графа на рис. 2.17 составить матрицу главных контуров.

Решение. Выбранное дерево (ветви 1-2--4) и контуры показаны на рис. 2.17. Номера контуров обозначаем римскими цифрами. Матрица контуров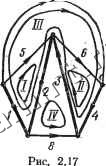

в = II
	0

Число строк матрицы В равно числу независимых контуров к. Если матрица контуров состаачена для бшьшего числа контуров, то ее обозначают Вц.

Второй закон Кирхгофа для напряжений в матричной форме записывают следующим образом:

60 ) = 0.

(2-9)

Токи всех ветвей могут быть выражены как линейные комбинации токов ветвей связи. Можно считать, что в каждом контуре замыкается контурный ток, равный току ветви связи этого контура. Если элементы /-го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока /-Й ветви через контурные токи (через токи ветвей связи). Этот результат может быть записан в виде матричного соотношения

(2.10)

где -столбцовая матрица контурных токов.

Если ветвям дерева присвоены первые номера, то матрица главных контуров состоит из двух подматриц:

B = [-F 1],

где F -подматрица матрицы сечений Q, составленная на основании того же самого дерева (см. примеры 2.3 и 2.4); 1-еда-ничная подматрица порядка к = в - у+1.

пример 2.5. Проиллюстрировать матричные соотношения (2.5)-f-.(2.10) на примере графов рис. 2.15 ч-2.17.

Решение. Матриш ! А и В графов на рис. 2.15-j-2.17 записаны в примерах 2.24-2.4. Матрицы токов и напряжений ветвей содержат по восемь элементов:

ffB)-

	; и =
		. 8-

Выполняя умножение матрицы А на матрицу i, легко получить уравнения ,

(1 + Б + 7=0; а-is- 6+ 6=0; 4- в- 7=0;

3 -4 - 8=0.

которые, как видно из графа на рис. 2.15, представляют собой уравнения по первому заколу Кирхгофа для узлов J, 2, 3 а 4,

Умножая матрицу Q на матрицу i , можно получить уравнения по первому закону Кирхгофа для сечении на рис. 2.16:

2 - 6-V- 8=0; 3- в-7- 8 = 0;

4- 6- 7= О.

в правильности этих уравнении нетрудно убедиться нрпосрелственно из рассмотрения графа на рис. 2.16.

Умножение матрицы В на матрицу и дает уравнения по второму закону Кирхгофа для контуров на рис 2.17:

- 1 + 2+ 5=0; з + 4 + б = 0;

- l + 2 + W8 + 4-- 7 = 0; 2--Из + 8=0-

Для иллюстрации соотношений (2.6), (2.8) и (2.10) необходимо записать матрицы узловых потенциалов, напряжений ветвей дерева и контурных токов:

Матрица ц> содержит потенциалы всех узлов, кроме фб=0, поскольку d матрице А (см. пример 2.2) отсутствует строка, соответствукяцая узлу 5. Произведение

	и ----
-Ф4-		- 4-		.IV.

					ф1
					-ф4-

Умножая матрицы, получим соотношения:

1=ф1; 2=ф2; з=-Фа+ф4; 4=

S-Ф4; б=ф1-

в = ф2 -фз; 7=ф1 -фз; 8 = -ф4-

Справедливость этих равенств очевидна (см. рис. 2.15). Аналогично при умножении матрицы на матрицу ui получаются выражения:

i= i; 2= г; з= з; j= 4; 6= i-

7 = l - 2- 3 - 4; 8 = - ;

в=т- 3 - 4;

2- 3-

Первые четыре равенства определяют напряжения ветвей дерева, осталь1 ные - напряжения ветвей связи через напряжения ветвей дерева. Правильность этих равенств очевидна из рис, 2.16.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [ 17 ] 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.