
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи где е и J - столбцовые матрицы напряжений источников э. д. с. и токов источников тока; матр-йцы Нес, icL и другие определяют связь между соответствующими переменными в схеме на рис. 15.20. Например, при it = 0, е = 0 и J = О из первого уравнения системы (15.31) получаем \c = HccUc; следовательно, элементы матрицы Нес представляют собой входные и взаимные проводимости ветвей с источниками uc- Аналогично можно убедиться, что элементы матриц Нее являются входными и взаимными проводимостями ветвей с источниками uc и е; элементы матриц Hci, Не/-коэффициенты передачи тока соответствующих ветвей; элементы матриц Hic. Hie - коэффициенты передачи напряжения; элементы матриц Hil сопротивления соответствующих ветвей. Уравнения (15.31) можно переписать в виде 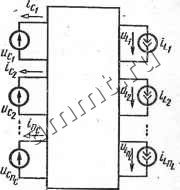 Рис. 15.20 и Hij-входные и взаимние Чгг Н Hic Hi Hce Hci H, H (15.32) Приравнивая правые части уравнений (15.30) и (15.32),. получаем уравнение Нес Hci Hic Hii T-lf Hce 4cj Hi Ни (15.33) Данное уравнение совпадает с (15.28), если принять:
(15.34) (15.35) Уравнение (15.29) для выходных переменных также можно составить по принципу наложения. Если где il, 2 -столбцовые матрицы соответственно выходных токов и напряжений, то по аналогии с уравнением (15.32) Hic Hii Нас Hai, Hie Ни L ae H90 На/ (15.36) где элементы матриц Hic, Hi, Нас, Hat, ttte. Ни, Нае, На/ представляют собой соответственно входные и взаимные проводимости, коэффициенты передачи тока, входные и взаимные сопротивления, коэффициенты передачи напряжения соответствующих ветвей. Таким образом, в уравнении (15.29) Hic Ни Но/- Но Ва = 21J Hie Hi/ LHae Ha/j [(15.37) (15.38) Пример 15.8. Составить уравнения вида (15.28) и (15.29) для цепи на рис. 15.21, а с помощью принципа наложения. 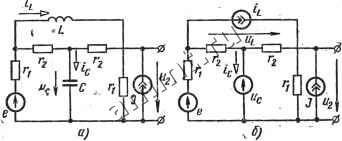 Рис. 15.21 Решение. Пусть тогда общие уравнения (15.32) и (15.36) принимают вид
2 = [2С 2j Заменяя емкость источником э.д. с, а индуктивность-источником тока (рис. 15.21, б), определим Н,, и т. д. Сначала в схеме на рис. 15.21, б исключим источники ij, е, /, т. е. при мем ii=0, е-0 и /=0. Тогда =0; и-. -i- г: И/ = -v- г и, следовательно. Если tjrO, ttcO, е=0 и J =0, то l + -a l + 2 поэтому -=0; Н 21 = 1 + 2 Полагая в схеме на рис. 15.21, б ,=0, =0, /=0; е=5&0, наидем! I ri + ri 1 е; ы =0; При е=0, £,=0, tj.=0, J фО П i+г i + -a х + -г г1г2 г1+г2 2/ = J г1 + г2 Матрицы А( и Bi вычислим в соответствии с выражениями (.15.34) и (15.35), учитывая равенство
В результате уравнения (15.28) и (15.29) принимают вид С(гг + г,) О 2 = b(ri+r2)J /1 х-г С(Г1 + г Г1Гг Х(/-1 + А2) L(ri+r Л + Ч Ах+-г. О , Применение топологических соотношений. Рассмотренная методика составления уравнений (15.28) и (15.29) с помощью принципа наложения непригодна, если в схеме цепи имеются емкостные контуры и индуктивные сечения, так как в таком случае нельзя записать уравнение (15.32). Для произвольных цепей (с емкост-ньми контурами, индуктивными сечениями, а также электронными элементами), если воспользоваться топологическими матрицами сечений и контуров, уравнениями Кирхгофа в матричной форме и уравнениями для схемных элементов, могут быть составлены уравнения состояния. Уравнения состояния произвольных цепей можно привести к виду (15.28). При этом в правой части появятся дополнительные слагаемые, содержащие производные от напряжений
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |