
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи ГЛАВД 8 ТОПОЛОГИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ЦЕПЕЙ, СОДЕРЖАЩИХ ДВУХПОЛЮСНЫЕ ЭЛЕМЕНТЫ БЕЗ ВЗАИМНОЙ ИНДУКЦИИ § 8.1. Топологические формулы для расчета определителей матриц узловых проводимостей и проводимостей сечений Топологическая формула для расчета определителя матрицы узловых Проводимостей. Определитель определенной матрицы узловых проводимостей, называемый в целях краткости узловым определителем А, равен сумме произведений проводимостей ветвей всех деревьев схемы: А<-=Е (8.1) где YjiYj2... У} {у 1) - произведение проводимостей ветвей /-го дерева, Пд -число всех возможных деревьев схемы.. Выражение (8.1) представляет собой топологическую формулу для расчета узлового определителя. Доказательство формулы (8.1) следует из равенства (7.30), согласно которому узловой определитель вычисляют как определитель произведения матриц: А(У) = det (AY<)At). Если обозначить AY< > = Pi, AfPa, то Ay = detPiP2. В теории матриц доказывается следующая теорема об определителе произведения двух матриц (теорема Бине -Коши): определитель произведения матрицы- Pi разжра тхп на матрицу Ра размера пхт {тп) равен сумж произведений всех соответствующих миноров максимального порядка tn матриц Pi и Pj. Здесь соответствующими называют миноры матриц Pi и Ра, которые образованы столбцами матрицы и строками матрицы Ра, имеющими одинаковые номера. Если минор матрицы Pi состоит из столбцов этой матрицы с номерами ki, ki, .... k, то соответствующий ему минор матрицы Ра должен состоять из строк этой матрицы с номерами ki, k, k. На основании сформулированной теоремы определитель А равен сумме произведений миноров максимального порядка матриц Pi = AY* и P2==Af, причем порядок миноров т - у~\. На величину определителя А влияют лишь миноры, отличные от нуля (ненулевые миноры). В гл. 2 было доказано, что все неособенные подматрицы порядка у - 1 матрицы А соответствуют деревьям схемы, а их определители равны ±1, т. е. все ненулевые миноры порядка у- 1 соответствуют деревьям схемы и равны it I. Так как Y - диагональная матрица,при умножении матрицы А на матрицу Y элементы k-ro столбца матрицы А умножаются на проводимость Fft /г-й ветви схемы. Элементам -f 1, - 1 и о в fe-м столбце матрицы А соответствуют элементы -Ь У*, - и о в k-u столбце произведения матриц AY\ Следовательно, все ненулевые миноры - порядка у - 1 матрицы Pi = AY соответствуют деревьям схемы. С помощью разложения /-го ненулевого минора можно доказать, что его величина равна произведению проводимостей ветвей /-го дерева, взятому с положительным (отрицательным) знаком: ± YjiYji, ... ... Уу,г, 1 (см. аналогичное доказательство величины ненулевого минора матрицы А, приведенное в гл. 2). . Ненулевые миноры порядка матрицы соответст- 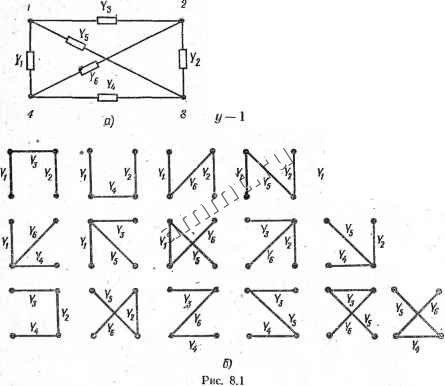 вуют деревьям схемы и равны ± 1, так как взаимная перестановка строк и столбцов не меняет величины минора. Знаки соответствующих ненулевых миноров матрицы Pi = AY* и = = А одинаковы (каждая пара миноров соответствует одному и тому же дереву), поэтому ;-е произведение соответствующих миноров равно произведению проводимостей ветвей /-го дерева, взятому с положительным знаком. Сумма произведений всех соответствующих миноров матриц AY и А равна сумме произведений проводимостей ветвей всех деревьев схемы. На рис. 8.1,0: показана схема, все деревья которой изображены на рис. 8.1,6. В соответствии с формулой (8.1.) определи- тель этой схемы ; Д(у) = YiYYs + УгПП + ГхКаУб + YYsY, + YYY + + + У1УзП+ YiY,Ye + Y2YnYe+ Г2ГзУ4 + 6+ + YiY.Y, + YY.Ye -f YY.Y, + YYY + Y,Y,Ye. Число деревьев схемы. Если применить теорему об определителе произведения двух матриц к произведению АА, то число деревьев схемы Од-= det (АА). (8.2) Действительно, соответствующие ненулевые миноры порядка у - 1 матриц А и А одинаковы и равны dt 1; число таких миноров совпадает с числом деревьев. Из формулы (8.1) вытекает еще один способ нахождения числа деревьев. Если проводимость каждой ветви схемы принять равной единице, то узловой определитель будет равен числу деревьев. Топологическая формула для расчета определителя матрицы проводимостей сечений. Ненулевые миноры порядка у-1 матрицы сечений Q, так же как и миноры узловой матрицы А, соответствуют деревьям схемы и равны zb 1 (см. гл. 2). Поэтому определитель матрицы проводимостей сечений А(=) = det QYCQ равен сумме произведений проводимостей ветвей деревьев схемы: A=> = i: ВД2...Г/,-1. (8.3) / =1 Таким образом, А(у> = А<>. Равенство определителей А и А<=> можно доказать непо-q)eACTBeHHo из выражений для матриц Y* и Y>. Матрица проводимостей- сечений гдеО = АдА. Следовательно, Y(=) = AflAYCA- (Ад)- = АдУ(у) (Aд ) где Y(y) = AY()A\ Матрицы А , \у\ (Ад)- являются квадратными. Известно, что определитель произведения квадратных матриц равен произведению их определителей *, поэтому det Y= = det Ад det Y<y) det (Ад)\ Определитель подматрицы Ад, соответствующей дереву, равен 1. Отсюда det Y(<=) = (±i)det Y(y)(±l) = detY(y). . * Для двух квадратных матриц сформулированное положение можно рассматривать как частный случай теоремы Бнне - Кошн.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |