Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 [ 139 ] 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

Выражению (15.17) можно придать другую форму, если под знаком интеграла переменную t - % заменить на т:

i{t)=u{Q)g{t)-\-\u {t-i)g{T)dx. (15.18)

Чтобы получить соотношения для расчета реакции цепи с помощью импульсной характеристики, заданное напряжение (рис. 15.9) следует представить как совокупность импульсов длительностью Ат. Площадь одного импульса можно считать равной произведению м(йДт)Дт. Если каждый импульс заменить импульсной функцией м(йДт) Атб(г -йДт), то

u(t)pu{k%)xЬ{t-k%).

Реакция цепи на импульс м (А Ат) Атб - й Ат) определяется как произведение

ы (й Дт) g6 - ft Ат) Дт,

где g(,{t - ktsx) - viMnyjibman характеристика. По. принципу нало-. жения реакция цепи на напряжение и {t) выражается соотношением

. i{t)=Yi)S(i{* - kl1)x,

или при Ат->-0

t

t(t)=\u{x)g{t-x)dx. (15.19)

Учитывая равенстю (15.14), формулу (15.19) можно также записать в виде

i(t) = \u{:c)g(t-x)dx. (15.20)

Если переходная характеристика g{t) имеет разрыв в точка t=0, то она может быть представлена в виде суммы:

g(0 = (0) 1(0+1(0.

где gl {t) = g{t) - g (0) при г > 0. В этом случае импульсная характеристика

gb{t-x)=g(t-x) = g{Q)b{t-x)-gi{t-x),

ёИ -т)=§-( -т) при <>т, т.е. содержит импульсную функцию g(0)6(<-T). Из выражения (15.20)

i{t)g{Q)u{t)-{u{:t)gil-x)dx. (15.21)

Равенство (15.21) можно доказать на основании (15.17), если применить формулу интегрирования по частям. Заменяя под знаком интеграла в соотношении (15.21) переменную г - X на т, можно получить еще ддно соотношение

i{t) = g(0)ujt) +lu(t-T)g(т)dx. (15.22)

Формулы (15.16)-н (15.22) называют интегралами Дюамеля или интегралами наложения.

Пример 15.5. Определить ток в последовательной /L-цепи при подключении к источнику импульсного напряжения (рис 15.10). Решение. В интервале времени О -г- напряжение и ф изменяется по линейному закону

(0=1

и производная и(t)=U/ti постоянна. Для расчета тока воспользуемся соотношением (15.16). Переходная проводимость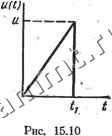

следовательно.

i(0 = 5 {T)g(f-T)dT=:

l-e---

В интервале времени t:>ti напряжение u(f)=0. С учетом разрыва функции u{t) в момент t=ti

кг I

1-е

-t)

При t=k решения, найденные для различных интервалов, дают одно и tro же значение тока i {к).

§ 15.4. Особенности расчета переходных процессов в цепях о емкостными контурами и индуктивными сечениями

В схеме электрической цепи в результате коммутации могут бьггь образованы контуры, которые состоят только из емкостей или емкостей и источников э. д. с. (емкостные контуры). Если

контур состоит только из емкостей, то в первый момент после коммутации, по уравнению Кирхгофа, ис(0+) = 0, гце uc -

напряжение на k-й емкости контура. Считая напряжение на емкости ис (0+) = ыс (0 ) непрерывным, легко прийти к противоречию: для произвольных начальных условий 2 Сд. (0 ) О, однако

2 c,(0.) = 0.

Аналогично в результате коммутации в схеме могут быть образованы сечения, состоящие только из индуктивностей или из индуктивностей и источников тока (индуктивные сечения). Если сечение состоит только из индуктивностей, то, согласно закону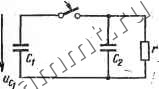

Рис. 15.11

Рис. 15.12

Кирхгофа, 2 (*+) ~ индуктивности сечения.

Для произвольных начальных условий 2] -ь О поэтому

при условии непрерывности токов в индуктивностях i (0+) = == (0 ) также возникает противоречие.

В схеме на рис. 15.11 емкость Ci, заряженная до напряжения и, присоединяется к незаряженной емкости Сг, образуя емкостной контур - Cg. До коммутации с, (0 ) = UUc (0 ) = = 0; после коммутации uc, (0+) = mcj (0+). В схеме на рис. 15.12 после коммутации индуктивности и включаются последовательно, образуя индуктивное сечение Li - L. До коммутации il (0 ) = e/rj ф (0-) = 0; после коммутации Ji (0+) = (0+).

Таким образом, при расчете схем с емкостными контурами или индуктивными сечениями нельзя применять условия непрерывности напряжений на емкостях или токов в индуктивностях (законы коммутации). В таких случаях следует применять более общие условия (законы): условия сохранения заряда и потокосцепления.

Условие сохранения (непрерывности) заряда для схемы на рис. 15.11 имеет вид

(71 (0 ) -Ь (0-) = (71 (0+) -f (72 (0+),

где (7i = Ci c (72 = СгСг - заряды емкостей Ci и Сг, т. е. суммарный заряд емкостей Ci и Cg непрерывен в момент коммутации.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 [ 139 ] 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.