
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation Не обводятся наборы, состоящие только из клеток, помеченных буквой d. Если бы соответствующие термы-произведения были приняты во внимание, то это привело бы к ненужному увеличению стоимости реализации. В примере на рис. 4.37 таких термов-произведений два: N3 N2 и Ыз N ь Как обычно, не обводятся никакие клетки, содержащие 0. (Это просто напоминание.) Остальная часть процедуры - та же, что и раньше. В частности, мы ищем особенные клетки, содержащие 1, и не особенные клетки, помеченные буквой d, и включаем в составляемое логическое выражение только существенные простые импликанты и такие другие импликанты, которые необходимы, чтобы покрыть все единицы на карте. В примере на рис. 4.37 двух существенных простых импликант достаточно, чтобы покрыть все единицы на карте. При этом оказываются покрытыми также две клетки, помеченные буквой d, так что при безразличных комбинациях переменных 10 и 11 функция F будет иметь значение 1, а при других безразличных комбинациях переменных-О, (а) N, (Ь) 43 2 N, No\ 00 00 01 11 10
Nj-N 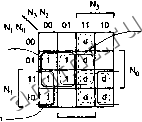 N2-No F = £n3.N2.N1.No(1.2,3,5,7) + d(10,11,12,13,14,15) rNg-No-bNz-N, Рис. 4.37. Устройство для обнаружения простых чисел в двоично-десятичном представлении: (а) исходная карта Карно; (Ь) карта Карно с простыми импликантами и особенными клетками, содержащими 1 Некоторые языки описания схем, в том числе язык ABEL, содержат средства, с помощью которых разработчик указывает безразличные комбинации входных сигналов, и программа логической минимизации учитывает эти комбинации при нахождении минимальной суммьь *4.3.8. Минимизация схем со многими выходами На практике у большинства комбинационных логических схем число выходов бывает больше одного. Задачу минимизации схемы с п выходами всегда можно свести к решению и независимых задач с единственным выходом. Однако, поступая так, мы можем пропустить те или иные возможности оптимизации. Рассмотрим, например, следующие две логические функции: F =IxYz(3,6, 7) G = ,xz(0b3). На рис. 4.38 представлена схема с выходами F и G, получающаяся в результате решения двух независимых задач минимизации схем с одним выходом, относя- щихся к функциям F и G порознь. Однако, как показано нарис. 4.39, можно найти также такую пару выражений вида сумма произведений , в каждую из которых входит один и тот же терм-произведение, в результате чего получается схема, содержащая на один вентиль меньше, чем в первоначальном варианте. XY X z\ 00 01 11 10 yz - 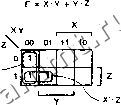 -j F =xy + y-; - G = xY- + x-; G = X-Y + XZ Рис. 4.38. Задача о проектировании схемы с двумя выходами, рассматриваемая как две независимые задачи о построении схем с одним выходом: (а) карты Карно; (Ь) минимальная схема (а) X
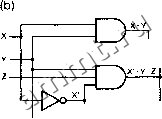 L-- F = XY + XY-2 4>x I-V Ц \ G =x--y- + X-y-2 Рис. 4.39. Минимизация схемы сдвумя выходами: (а) минимизируемые карты и выделение общего терма; (Ь) минимальная схема, составленная с учетом двух выходов При проектировании комбинационных схем со многими выходами на основе отдельных вентилей, как это имеет место в случае специализированных ИС, наличие общих термов-произведений очевидным образом приводит к уменьшению размера схемы и ее стоимости. Кроме того, в ПЛУ структура, реализующая сумму произведений, повторена много раз, и мы знаем теперь, как минимизировать такую структуру отдельно для каждого выхода; в некоторых ПЛУ допускается со- вместное использование термов-произведений схемами, относящимися к разным выходам. Идеи, излагаемые в этом разделе, использованьЕ во многих профаммах логической минимизации. Возможно, что в примере, приведенном на рис. 4.39, вы смогли непосредственно углядеть минимальное решение, рассматривая карты Карно для функций F и G. Однако минимизацию схем большего размера можно осуществить только путем применения формального алгоритма минимизации для случая многих выходов. Сейчас этот алгоритм в общих чертах будет описан; подробнее с ним можно ознакомиться по литературе. Ключом к успешной минимизации схемы со многими выходами, описываемой набором из и функций, является рассмотрение не только самих исходных п функций, относящихся к отдельным выходам, но также и функций-произведений , т-прошведением {m-product function) для набора из п функций называется функция, являющаяся произведением т функций, где 2< т < п. Существует 2 - п - 1 таких функций. В нашем примере, к счастью, и = 2 и есть только одна функция-произведение F G, которую надо рассматривать. На рис. 4.40 повторены карты Карно для функций F и G и приведена карта Карно для F G; в общем случае карта для /я-произведения получается путем операции И над картами всех т его компонент. Простая импликанта схемы со многими выходами (multiple-output prime implicant) для набора из п функций - это простая импликанта одной из п функций или одной из функций-произведений. Первый шаг минимизации в случае многих выходов состоит в нахождении всех простых импликант схемы со многими выходами. Каждая простая импликанта /и-произведения является кандидатом на включение в логические выражения, относящиеся к соответствующим т выходам схемы. Если бы мы попытались минимизировать набор из 8 функций, мы должны были бы найти простые импликанты для 2* - 8 - 1 = 247 функций-произведений, а также для 8 заданных функций. Очевидно, что минимизация схемы со многими выходами - занятие не для слабонервных! После того, как простые импликанты схемы со многими выходами найдены, мы пытаемся упростить задачу, выбирая существенные среди них. Особенной клеткой, содержащей 1 (distinguished 1-cell), на карте, относящейся к той или иной функции одиночного выхода F, называется содержащая 1 клетка, которая покрывается точно одной простой импликантой функции F или простой импликантой одной из функций-произведений, в которые входит F. На рис. 4.40 особенные клетки, содержащие 1, заштрихованы. Существенной простой импликантой (essentialprime implicant) определенной функции одиночного выхода является простая импликанта, покрывающая особенную клетку, содержащую 1. Как и в случае минимизации с одним выходом, существенньЕе простые импликанты должны быть включены в решение, обеспечивающее минимальную стоимость реализации. В остающейся части алгоритма речь идет только о клетках, содержащих 1, не покрываемых существенными простыми импликантами. Заключительный этап состоит в выборе минимального набора простых импликант, чтобы покрыть остающиеся клетки, содержащие 1. На этом этапе мы должны рассматривать все п функций одновременно, включая возможность совместного использования одних и тех же компонентов; детали этой процедуры ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||