
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation 4.20. Повторите упражнение 4.19 и найдите минимальные выражения вида произведение сумм для каждой логической функции. 4.21. Для каждой логической функции из двух предыдущих упражнений проверьте равенство минимальных выражений вида сумма произведений и вида произведение сумм . Сравните также стоимость реализации выражений того и другого вида. 4.22. Дм каждого из следующих логических выражений найдите все статические источники опасности в соответствующей двухуровневой схеме И-ИЛИ или ИЛИ-И и постройте свободную от источников опасности схему, реализующую ту же самую логическую функцию: (a) F = W - X + W Y (b) F = W X Y + X Y Z + X Y (c) F = WY + XY + W XZ (d)F = WX+YZ+WXYZ+WXYZ (e) F = (W + X+Y) (X + Z) (f) F=(W + Y + Z)-(W + X + Z)-(X + Y + Z) (g)F = (W + Y+Z)-(W+X + Y+Z)-(X + Y)-(X+Z) 4.23. Запищите набор проверочных векторов на языке ABEL для устройства из табл. 4.17, обнаруживающего простые числа. 4.24. Напищите VHDL-программу (объект и структуру) для изображенной на рис. 4.19 схемы охранной сигнализации в стиле структурного проектирования. 4.25. Сделайте то же самое, что и в упражнении 4.24, в стиле потокового проектирования. 4.26. Сделайте то же самое, что и в упражнении 4.24, в стиле поведенческого проектирования. 4.27. Напишите структурную VHDL-программу, соответствующую изображенной нарис. 5.17 логической схеме, построенной на основе вентилей И-НЕ. Задачи 4.28. Придумайте не тривиально выглядящую логическую схему с обратной связью, но такую, у которой выходной сигнал зависит только от текущего значения входного сигнала. 4.29. Докажите теорему объединения Т10, не используя полной индукции, но предполагая, что теоремы Т1-Т9 и ТГ-Т9 верны. 4.30. Покажите, что теорема объединения Т10 является всего лишь частным случаем согласованности (теорема Т11) с учетом поглощения (теорема Т9). 4.31. Докажите, что (X + Y) Y = X Y, не используя метод полной индукции, но предполагая, что теоремы Т1-Т11 и ТГ-Т1Г верны. 4.32. Докажите, что (X + Y) (X + Z) = X Z + X Y, не испочьзуя метод полной индукции, но предполагая, что теоремы Т1-Т11 и ТГ-Т1Г верны. 4.33. Покажите, что и-входовой вентиль И можно заменить и -1 двухвходовыми вентилями И. Можно ли утверждать то же самое относительно вентилей И-НЕ? Объясните свой ответ 4.34. Сколько существует физически различных способов реализащ1и логического выражения V W X Y Z на четьфех двухвходовых вентилях И (типа 74x08)? Объясните свой ответ. 4.35. Докажите по правилам алгебры переключений, что в результате объединения двух входов (и + 1)-входового вентиля И или ИЛИ получается функциональный эквивалент и-входового вентиля. 4.36. Докажите по индукции теоремы Де Моргана (Т13 и Т13). 4.37. Какое из условных обозначений ТТЛ-вентиля ИЛИ-НЕ - на рис. 4.4(c) или (d) - точнее отражает его внутреннее устройство? Почему? 4.38. Используя теоремы алгебры переключений, преобразуйте следующее выражение так, чтобы в нем было возможно меньшее число инверсий (допускается инвертирование того, что заключено в скобки): В С + А С D + А С + Е В + Е (А + С) (А + D). 4.39. Докажите справедливость или ошибочность следующих утверждений: (a) Пусть А и В - логические переменные. Тогда из равенств А В = О и А + В = 1 следует, что А = В. (b) Пусть X и Y - логические выражения. Тогда из равенств X Y = О hX+Y= 1 следует, чтоХ = У. 4.40. Докажите теоремы расширения Шеннона. (Указание: Не пугайтесь, это легко.) 4.41. Теоремы расширения Шеннона можно обобщить, распространив их на случай не одной, а / переменных; из этого следует, что логическую функцию можно представить в виде суммы или произведения 2 членов. Сформулируйте обобщенные теоремы расширения Шеннона (generalized Shannon-expansion theorems). 4.42. Покажите, как с помощью обобщенных теорем расширения Шеннона придти к представлению функций в виде канонической суммы или канонического произведения. 4.43. Вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ (Exclusive OR gate; XOR) - это двухвходовая логическая схема, на выходе которой логическая I появляется тогда и только тогда, когда точно один из сигналов на ее входах равен 1. Составьте таблицу истинности для логической функции ИСКЛЮЧАЮЩЕЕ ИЛИ, запишите ее представление в виде суммы произведений и нарисуйте соответствующую схему вида И-ИЛИ. 4.44. Какую функцию, с точки зрения алгебры переключений, выполняет двухвходовой вентиль XOR, у которого входы соединены вместе ? В чем состоит возможное различие между выходными сигналами реального вентиля XOR и идеального элемента, реализующего ту же логическую функцию? 4.45. Спроектировав и изготовив цифровую систему на базе ИС малой степени интеграции, разработчик обнаружил, что необходимо добавить еще один инвер- тор. В системе имеются следующие резервные логические схемы. 3-входовой вентиль ИЛИ, 2-входовой вентиль И и 2-входовой вентильХОВ. Как следует осуществить инвертирование, не добавляя еще одну микросхему? 4.46. Множество логических элементов различного типа называют полным {complete set), если с их помощью можно реализовать любую логическую функцию. Например, двухвходовые вентили И, двухвходовые вентили ИЛИ и инверторы образуют полное множество, поскольку любую логическую функцию можно представить в виде суммы произведений переменных и их дополнений, а функции И и ИЛ И с любым числом переменных можно реализовать на двухвходовых вентилях. Является ли полным множество, состоящее из одного логического элемента И-НЕ? Докажите ваще утверждение. 4.47. Является ли полным множество, состоящее из одного логического элемента ИЛИ-НЕ? Докажите ваще утверждение. 4.48. Является ли полным множество, состоящее из одного логического элемента XOR? 4.49. Дайте определение двухвходового вентиля, отличающегося от схем И-НЕ, ИЛИ-НЕ и XOR, который сам по себе образует полное множество, если допускается наличие постоянных входных сигналов, равных О и 1. Приведите соответствующее доказательство. 4.50. Некоторые думают, что существует четыре основных логических функции: И, ИЛИ, НЕ и вит. Нарис. Х4.50 приведено возможное условное обозначение вентиля BUT {BUTgate) с 4-мя входами и 2-мя выходами. Придумайте полезную, нетривиальную функцию, которую мог бы выполнять вентиль вит. Эта функция должна быть так или иначе связана со смысловым значением названия схемы (англ. but означает но ). Следует иметь в виду, что симметричность условного обозначения предполагает симметрию функции по отнощению ко входам А и В в верхней и нижней частях схемы и по отношению к выходам схемы Z1 и Z2. Опишите словами вашу функцию BUT и составьте для нее таблицу истинности. РИС.Х4.50 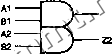 4.51. Запишите логические вьфажения для выходных сигналов Z1 и Z2 вентиля BUT, разработанного вами в предыдущей задаче, и нарисуйте соответствующую принципиальную схему, состоящую из вентилей И и ИЛИ и инверторов. 4.52. Большинство учащихся не испытывают никаких затруднений при преобразовании логического выражения согласно теореме Т8 путем разнесения множителя по слагаемым , однако многих ставит в тупик преобразование логического выражения согласно теореме Т8 путем разнесения слагаемого по сомножителям . Как можно воспользоваться двойственностью, чтобы преодолеть такое затруднение? ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |