
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation CLOCK внешние входы 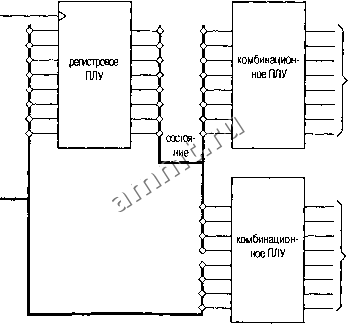 выходы типа Мура выходы типа Мили Рис. 9.2. Разбиение конечного автомата по трем ПЛУ С другой стороны, при записи состояний в форме выходного кода (см, раздел 7.3.2) требуется меньшее обшее число выходов ПЛУ. Используя такое представление состояний, автомат, управляюший задними огнями автомобиля, можно разместить в одной ИС 16V8, как мы увидим это в разделе 9. L3. Аналогично любой переменной состояния или выходу типа Мура, переменная состояния, записанного в форме выходного кода, принимает установившееся значение спустя время t после фронта тактового сигнала. Следовательно, представление состояния в форме выходного кода позволяет повысить быстродействие и обеспечивает большую эффективность компоновки. При управлении задними огнями автомобиля включение аварийной сигнализации на 10 не раньше не существенно, однако в высококачественной цифровой системе лишние 10 не задержки могут вызвать уменьшение максимальной частоты системного тактового сигнала со 100 МГц до 50 МГц. При необходимости размещения системы в двух или большем числе ПЛУ лучше всего - с точки зрения простоты проекта и эффективности использования микросхем - осуществлять разбиение так, как показано на рис. 9.2. Единственное пос-ледовательностное ПЛУ применяется для того, чтобы обеспечить требуемые переходы из одного состояния в другое. С помощью комбинационных ПЛУ из переменных состояния и входных сигналов формируются значения сигналов на выходах типа Мили и типа Мура. число единиц 9.1.2. Несколько простых автоматов в парафафе 7.4 мы построили несколько простых конечных автоматов традиционными методами. В табл. 7.25 проект, относящийся к первому из них, был представлен на языке ABEL в расчете на реализацию в ПЛУ, а затем в табл. 7.27 было показано, как лучше воспользоваться особенностями языка ABEL, чтобы поведение автомата сделать более понятным. Наш второй пример - автомат для подсчета числа единиц , к которому предъявляются следующие фебования: Должен быть построен тактируемый синхронный конечный автомат с двумя входами X и Уи одним выходом2. Сигнал на выходе должен равняться 1,если число единиц, поступивших на входы X и Y с момента запуска, кратно 4; в противном случае сигнал Z должен равняться 0. Таблица состояний для этого автомата уже была нами составлена (см. табл. 7.12). Однако функции такого автомата значительно легче выразить средствами языка ABEL, как это видно из табл. 9.1. Заметьте, что в данном случае лучше воздержаться от использования синтаксиса диафамм состояний языка ABEL. Функцию этого автомата естественнее выразить с помощью вложенного оператора WHEN и всфоен-ной операции суммирования. Первым предложением WHEN автомат устанавливается в его начальное состояние и счет сбрасывается в О, а в последующих предложениях счет увеличивается на 2, на 1 или на О при вьшолнении соответствующих условий, когда автомат не пребывает в сброшенном состоянии. Заметьте, что по правилам языка ABEL при сложении бит переноса теряется , что эквивалентно выполнению сложения по модулю 4. Этот автомат легко умещается в ПЛУ GAL16V8. У него четыре состояния, поскольку он реализуется на двух фиггерах. Табл. 9.1. Програм- iKodule onesctsm зые abl title Ones-counting State Machine для конечного авто- ONESCTSM device P16V8R; ата считающего Inputs and outputs CLOCK, RESET, X, Y pin 1, 2, 3, 4; Z pin 13 istype com; COUHTl..COUKTO pin 14, 15 istype reg Sets COUNT = [COUNT1..COUNTO]; equations COUNT.cue - CLOCK; WHEN RESET THEN COUMT := 0; ELSE WHEN X & Y THEN COUNT := COUNT + 2; ELSE WHEN X # Y THEN COUNT := COUNT + 1; ELSE COUNT := COUNT; Z = (COUNT == 0); end oneset8ш ОТКАЖЕМСЯ ОТ ДУРНЫХ ПРИВЫЧЕК! В главе 7 мы начали проектирование автоматов с помощью таблиц состояний, не включая явно вход сброса. У этого были две причины: во-первых, с каждым дополнительным входом, в принципе, удваивается работа, которую необходимо выполнить для синтезирования конечного автомата вручную, а во-вторых, с педагогической точки зрения, это давало бы небольшой эффект. Но в реальных проектах практически всегда требуется вход сброса, сигнал на котором обеспечивает возврат автомата в известное состояние. Поэтому теперь, переходя к разработке конечных автоматов путем описания на том или ином языке и с помощью автоматизированных средств, мы должны отказаться от дурной привычки и обеспечивать наличие входа сброса в явном виде. Другой пример из параграфа 7.4 - конечный автомат для кодового замка (в дальнейшем опущен выход HINT, имевшийся в исходном варианте): Построить тактируемый синхронный конечный автомат с одним входом X и одним выходом UNLK. Сигнал на выходе UNLK должен равняться 1 тогда и только тогда, когда сигнал X равен О и последовательность его значений на предыдущих семи тактах имела вид: 011011L Нами была составлена таблица состояний для такого автомата (табл. 7.14) и написана эквивалентная профамма на языке ABEL (табл. 7.31). Однако мы снова применим другой подход, который легче понять. Заметим, что в этом примере сигнал на выходе автомата в любой момент времени полностью определен значениями входного сигнала на последних восьми тактах. Следовательно, мы можем воспользоваться так называемым принципом конечной памяти , когда явно отслеживаются семь предыдущих значений входного сигнала и выходной сигнал формируется как комбинационная функция этих значений. Профамма на языке ABEL в табл. 9.2 является реализацией принципа конечной памяти. В ней используются наборы, благодаря чему ее легко настраивать на другие кодовые комбинации. Заметьте, однако, что и в данном случае сформировать сигнал HINT было бы так же трудно, как и в исходной версии этого автомата (см. задачу 9.2). ПРИНЦИП КОНЕЧНОЙ ПАМЯТИ Возможно следующее обобщение идеи построения автомата с конечной памятью. Сигналы на выходах такого автомата полностью определяются текущими значениями входных сигналов и значениями выходных сигналов на последних п тактах, где п - конечное, Офаниченное целое число. Автоматом с конечной памятью является любое устройство, которое можно реализовать так, как показано на рис. 9.3. Заметьте, что автомат с конечным числом состояний не обязательно представляет собой автомат с конечной памятью. Например, у автомата, считающего число единиц, всего четыре состояния, но он не является автоматом с конечной памятью: его выходной сигнал зависит от всех значений X и Y с момента запуска. ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |