
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation сел в дополнительном коде (см. задачу 7.72). Кроме того, схема обнаружения нуля для системы чисел, представленных в обратном коде, должна либо проверять обе возможности, либо всегда преобразовывать 11- 11 в 00 00. *2.5.7. Представление чисел с избытком Да, действительно, различных способов представления отрицательных чисел так много, что можно говорить об их избытке, но все же есть еще один, о котором мы расскажем. При представлении с избытком В (excess-B representation) целого числа без знака М, значение которого удовлетворяет условию О < М< 2 , строка из т битов служит для выражения целого числа со знаком М-В, где В называется смещением (bias) данной числовой системы. Например, в системе с избытком 2 - (excess-2 system) любое число JT, принадлежащее интервалу от -2 - до +2 -1, представляется в двоичном виде т битами к.шХ+2 (эта последняя величина всегда неотрицательна и меньше, чем 2 ). Диапазон значений, которые могут быть представлены в такой системе, точно совпадает с множеством возможных значений двоичных т-разрядных чисел в дополнительном коде. В самом деле, вид любого числа в этих двух системах одинаков, за исключением знакового бита, значения которого в них всегда противоположны. (Это справедливо только в том случае, когда смещение равно 2 -.) Чаще всего представление с избытком применяется в числовых системах с плавающей точкой (см. Обзор литературы). 2.6. Сложение и вычитание двоичных чисел в дополнительном коде 2.6.1. Правила сложения Из табл. 2.6, где приведены десятичные числа и их эквиваленты в различных числовых системах, видно, почему представление в дополнительном коде является предпочтительным для выполнения арифметических операций. При счете в прямом направлении, начиная с числа 1000 (- 8,), каждое новое число в дополнительном коде вплоть до 0111 (+7,ц) можно получить из предыдущего, добавляя 1 и игнорируя перенос из 4-го разряда, когда он возникает. Этого нельзя сказать о представлении чисел в прямом коде со знаком и в обратном коде. Поскольку обычное сложение является развитием идеи подсчета, суммирование чисел в дополнительном коде (twos-complement addition) можно осуществить путем простого сложения двоичных чисел, пренебрегая переносами из старшего разряда. Результатом всегда будет правильное значение суммы, пока оно не выходит за допустимые пределы этой числовой системы. Приведем несколько примеров десятичного сложения и сложения двоичных чисел в дополнительном коде, подтверждающих сказанное: +3 + +4 +7 +6 + -3 ООП + 0100 0111 + 1101 +3 10011 + -6 1110 + 1010 -8 1 1000 +4 + -7 -3 0100 + 1001 1101 Табл. 2.6. Десятичные и 4-разрядные двоичные числа Десятичные числа Двоичные числа в дополнительном в обратном в прямом коде коде коде со знаком в коде с избытком 2
2.6.2. Графическая интерпретация На рис. 2.3 двоичная система чисел в дополнительном коде изображена иначе с помощью 4-разрядного счетчика . Здесь числа показаньЕ в циклической форме или в форме представления по модулю . Этот счетчик действует наподобие реального реверсивного счетчика, который будет рассмотрен в парафафе 8.4. Начиная с произвольного числа, на которое указывает сфелка, мы можем сложить его с +и, добавляя и раз по единице, то есть повернув указатель на и позиций по часовой стрелке. Очевидно также, что можно вычесть и из того или иного числа, отнимая и раз по единице, то есть повернув указатель на и позиций против часовой стрелки. Конечно, результат этих действий будет правильным только в том случае, когда и достаточно мало, так что мы не пересекаем разрыв между -8 и +7. Вычитание положительных чисел 1111 0000 0001 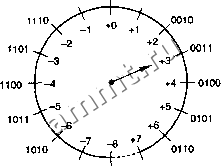 Сложение положительных чисел 1001 1000 0111 Рис. 2.3. Представление счета по модулю для 4-разрядных двоичных чисел в дополнительном коде Самое интересное здесь заключается в том, что мь[ можем вьЕчесть и (или прибавить -и), повернув указатель на 1 б - и позиций по часовой стрелке. Обратите внимание: величина (1 б - и) - это то, что мы назвали точным дополнением двоичного 4-разрядного числа и, то есть представлением числа-и в дополнительном коде. Эта фафическая иллюстрация свидетельствует в пользу утверждения о том, что представление отрицательных чисел в дополнительном коде позволяет складывать их с другими числами по обычным правилам сложения. Прибавление числа эквивалентно повороту указателя на рис. 2.3 на соответствующее число позиций по часовой стрелке. 2.6.3. Переполнение Если результат выполнения операции сложения вьеходит за предельЕ интервала чисел, представимых в данной системе, то говорят, что происходит переполнение {overflow). В примере нарис. 2.3 переполнение возникает при сложении положительных чисел, когда мы переходим через отметку +7. Сложение двух чисел с разными знаками никогда не может привести к переполнению, а сложение двух чисел с одинаковыми знаками может, как это видно из следующих примеров: -3 + -6 П01 1010 -9 10111 = +7 -8 1000 -8 + 1000 -16 10000 = +0 +5 + +6 +11 0151 + ОНО 1011 = -5 +7 0111 + +7 + 0111 1110 = -2 ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |