
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation САМОКОРРЕКТИРУЮЩИЕСЯ СХЕМЫ ОБЕСПЕЧИВАЮТ ИСПРАВЛЕНИЕ САМИ ПО СЕБЕ! Можно следующим образом доказать, что схема коррекции в самокорректирующемся счетчике Джонсона осуществляет исправление любого неправильного состояния. Неправильное состояние всегда можно представить в виде х...х10х...х, так как только нормальные состояния (00...00, И...И, 01...1, 0...01...1 и 0...01) нельзя записать в таком виде. Поэтому не более чем через и - 2 такта регистр сдвига будет содержать комбинацию 10х...х. На следующем такте его содержимое станет равным Ох...хО, и, такт спустя, в него будет зафужено нормальное состояние 00...01. У -разрядного счетчика Джонсона есть 2 -2и неправильных состояний, поэтому он также ненадежен, как и кольцевой счетчик. Но, как показано на рис. 8.67, можно построить самокорректирующийся счетчик Джонсона {self-correcting Johnson counter). В этой схеме происходит зафузка комбинации 0001 в качестве следующего состояния, если текущее состояние имеет вид ОххО. По такому же принципу с помощью одного 2-входового вентиля ИЛИ-НЕ можно осуществлять коррекцию в счетчике Джонсона с любым числом разрядов. Схема коррекции должна зафужать комбинацию 00...01 в качестве следующего состояния всякий раз, когда текущим оказывается состояние вида Ох...хО. +5 в CLOCK 74x194 >CLK -к) CLR LIN D С В A -iJRIN регистр сдвига, включенный на QD QC QB сдвиг влево QO QI Q2 Q3 74x02 74x04 Q3 L LOAD Рис. 8,67. Самокорректирующийся 4-разрядный счетчик Джонсона с 8 состояниями *8.5.8. Счетчики на регистрах сдвига с линейной обратной связью Число нормальных состояний у рассматривавшихся до сих пор счетчиков на п-разрядных регистрах сдвига бьшо далеко от максимально возможного числа состояний, равного 2 . Счетчик на основе и-разрядного регистра сдвига с линейной обратной связью {linear feedback shift-register, LFSR) имеет 2 - 1 состояний, то есть почти максимум. Такой счетчик часто называют генератором последовательности максимальной длины {maximum-length sequence generator). LFSR-счетчики строятся на основе теории конечных полей (finite fields), развитой французским математиком Эваристом Галуа (1811-1832) незадолго до того, как он был убит на дуэли его политическим противником. В работе LFSR-счетчика реализуются операции над 2 элементами в конечном поле. Нарис. 8.68 представлена структура и-разрядного LFSR-счетчика. На последовательный вход регистра сдвига поступает сумма по модулю 2 битов, содержащихся в определенном наборе разрядов регистра сдвига. Этой обратной связью определяется последовательность состояний, через которые проходит счетчик. Принято всегда нумеровать разряды так, как показано на рисунке, и считать, что сдвиг происходит в указанном направлении. CLOCK RESET L п-разрядныи регистр сдвига с параллельным выводом 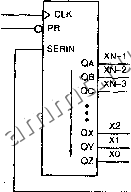 соединены с определенными выходами (см. таблицу) схема проверки на нечетность Рис. 8.68. Общая структура счетчика на основе регистра сдвига с линейной обратной связью В табл. 8.21 для ряда значений и приведены уравнения, описывающие цепь обратной связи в тех случаях, когда результирующая последовательность оказывается последовательностью максимальной длины. Для каждого значения и больше 3-х существует много других уравнений обратной связи, обеспечивающих генерирование последовательностей максимальной длины, причем различным уравнениям соответствуют разные последовательности. ДЕЙСТВИЯ В КОНЕЧНОМ ПОЛЕ Конечное поле содержит конечное число элементов, и в нем определены две операции - сложение и умножение, - удовлетворяющие ряду требований. Примером конечного поля с Р элементами, где Р - простое число, может служить совокупность целых чисел по модулю Р. Операциями в этом поле являются сложение и умножение по модулю Р. Согласно теории, конечные поля обладают следующим свойством: если вы начнете с ненулевого элемента Е и станете многократно умножать его на так называемый примитивный элемент а, то в течение Р ~2 шагов вы будете получать все другие ненулевые элементы поля, прежде чем снова возникнет элемент Е. Оказывается, что в поле с Р элементами любое целое число из интервала 2, Р ~ \ является примитивным элементом. Вы можете убедиться в этом сами, взяв, например, Р = 7 и а = 2. Элементами поля при этом являются числа О, 1, 6, а операциями - сложение и умножение по модулю 7. (Здесь автор ошибается: не все элементы 2, Р - \ являются примитивными; в частности, не является примитивным элемент 2. - Прим. перев.) В предыдущем абзаце приведена центральная идея, на которой основывается теория генераторов последовательностей максимальной длины. Но для того, чтобы этой идеей можно было воспользоваться применительно к цифровым схемам, нам необходимо поле с 2 элементами, где и-требуемое число разрядов. С одной стороны, нам повезло, так как Галуа доказал, что существуют конечные поля с / элементами при любом целом п, если только Р - простое число, включая случай Р = 2. Но, с другой стороны, приходится лишь сожалеть о том, что при п > 1 операции в полях с Р элементами (в том числе с 2 элементами) принципиально отличаются от обычных сложения и умножения целых чисел. Кроме того, труднее находить примитивные элементы. Если вы, как и я, любите математику, то, должно быть, вас приводит в восхищение теория конечных полей, на основе которой строятся генераторы последовательностей максимальной длины и другие LFSR-схемы (см. Обзор литературы). В противном случае, доверьтесь и следуйте рекомендациям этого параграфа по тому же принципу, по которому вы пользуетесь рецептами из Книги о вкусной и здоровой пище . i LFSR-счетчик со структурой, указанной на рис. 8.68, никогда не проходит в цикле через все возможные 2 состояний. Независимо от конфигурации соединений следующим состоянием за тем, при котором во всех разрядах находятся нули, является то же самое состояние с нулями во всех разрядах На рис. 8.69 показана принципиальная схема 3-разрядного LFSR-счетчика. Последовательность состояний этого счетчика приведена в левых трех столбцах табл. 8.22. Начиная с любого ненулевого состояния (в таблице - с состояния 100), счетчик проходит через семь состояний, прежде чем он возвращается в исходное состояние. ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |