
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation Код, применяемый для исправления ошибок, называется корректирующим кодом {error-correcting code). В общем случае справедливо правило: если минимальное расстояние в коде равно 2с+1, то с его помощью можно исправлять до с ошибок в битах (в предыдущем примере с = 1). Если минимальное расстояние кода равно 2с +d +1, то он позволяет исправлять до с ошибок и обнаруживать до d ошибок в других битах. На рис. 2.12(a) в качестве примера приведен фрагмент и-мерного куба для кода с минимальным расстоянием, равным 4 (с =1, =1). Единичные ошибки в словах 00101010 и 11010011, не являющихся кодовыми, можно исправить. Однако ошибки, приведшие к слову 101 ООО 11, исправить нельзя, поскольку это слово не может возникнуть в результате одиночной ошибки, а может лишь стать следствием искажения двух битов в одной из двух возможных пар ошибок. Таким образом, этот код позволяет обнаружить ошибку в двух битах, но не дает возможности исправить ее. Если принятое слово не является кодовым, то мы не знаем, какое именно кодовое слово в действительности было передано; мы знаем только, какое кодовое слово ближе всего к принятому. Следовательно, как показано на рис. 2.12(b), результат исправления тройной ошибки может оказаться неправильным. Подобного рода промахи бывают допустимы, если тройные ошибки происходят с очень малой вероятностью. С другой стороны, в случае, когда тройные ошибки следует принимать во внимание, можно изменить правило декодирования данного кода. Вместо того, чтобы пытаться исправлять ошибки, будем просто воспринимать слова, не являющиеся кодовыми, как содержащие ошибки. Тогда, как показано на рис. 2.12(c), тот же самый код с минимальным расстоянием, равным 4, позволяет обнаруживать до трех ошибок без их исправления (с =0, d =3). 2.15.3. Коды Хэмминга В 1950 году Хэмминг описал общий метод построения кодов с минимальным расстоянием, равным 3, которые теперь называют кодами Хэмминга {Hamming codes). Для произвольного / его метод дает (2-1)-разрядный двоичный код с / проверочными и 2-1-/информационными битами. Коды с меньшим числом информационных битов с минимальным расстоянием 3 получаются путем удаления информационных битов из кода Хэмминга с большим числом битов. Разряды в кодовом слове кода Хэмминга можно пронумеровать от 1 до 2-1. В этом случае, в разряде, номер которого является степенью 2, стоит проверочный бит, а в остальных разрядах помещаются информационные биты. Каждый проверочный бит вместе с некоторым подмножеством информационньЕх битов объединяются в одну группу согласно проверочной матрице {parity-check matrix). Как показано на рис. 2.13(a), в группу, относящуюся к каждому проверочному биту, попадают такие информационные биты, у которых номер позиции в двоичной записи содержит 1 в том же разряде, что и номер позиции данного проверочного символа. Например, проверочный бит с номером 2 (010) объединяется в одну фуппу с информационными битами с номерами 3 (011), 6 (110) и 7 (111). При заданной комбинации значений информационных битов значение проверочного бита выбирается по правилу четности; другими словами, полное число единиц в группе с этим проверочным символом должно быть четно. обнаруживаемые двойные ошибки 00101011 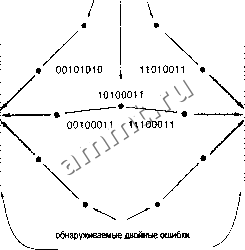 00101011 исправляемь№ одиночные ошибки 00101010 11010011 10100011 * 00100011 11100011 * тройная ошибка выглядит как одиночная ошибка 11000011 11000011 00101011 - обнаруживаемые одиночные, двойные и тройные ошибки 11000011 Рис. 2.12. Кодовые слова и слова, не являющиеся кодовыми, для 8-разрядного двоичного кода с минимальным расстоянием, равным 4: (а) исправление одиночных и обнаружение двойных ошибок; (Ь) ошибочное исправление тройной ошибки; (с) отказ от исправления ошибок взамен обнаружения до 3-х ошибок Имя группы группы Номер разряда 6 5 4 3 2 1 > Группы Номер разряда 7 6 5 3 4 2 1 -i-i- Проверочные биты > Группы Информационные биты Проверочные биты Рис. 2.13. Проверочные матрицы для 7-разрядного кода Хэмминга: (а) с расположением битов в порядке следования их номеров; (Ь) с разделением проверочных и информационных битов По традиции разряды в проверочной матрице и в самих кодовых словах бывают переставлены таким образом, чтобы все проверочные биты оказывались справа, как показано на рис. 2.13(b). В первых двух столбцах табл. 2.14 перечислены получающиеся в результате этого кодовые слова. Можно быть уверенным в том, что минимальное расстояние в коде Хэмминга равно 3, если в любом кодовом слове необходимо изменить, по крайней мере, 3 бита, чтобы получить другое кодовое слово. Другими словами, нужно убедиться в том, что изменение одного бита или двух битов в кодовом слове дает слово, не являющееся кодовым. Если изменить один бит ву-м разряде кодового слова, то нарушится условие четности в каждой из групп, в которую входитJ-й разряд. Поскольку каждый информационный бит содержится, хотя бы в одной группе, как минимум в одной из групп условие четности не будет выполнено и получающееся в результате слово не является кодовым. Что произойдет, если мы изменим два бита в у-м и к-и разрядах? В тех контрольных фуппах, которые содержат оба эти разряда, условие четности останется по-прежнему верным, поскольку оно не нарушается при изменении четного числа битов. Поскольку, однако,у и к различны, их выражения в двоичной записи отличаются, по крайней мере, в одном бите, соответствующем одной из контрольных групп. В этой группе изменится только один бит, в результате чего условие четности окажется невыполненным и получившееся слово не будет кодовым. ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |