
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation 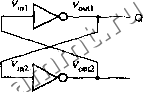 7.1.1. Цифровой подход Приведенную на рис. 7.2 схему часто называют бистабтьной (bistable), так как посредством формального щ1фрового анализа устанавливается, что у нее есть два устойчивых состояния. Прежде всего видим, что если на выходе Q имеет место высокий уровень, то, будучи подан на вход нижнего инвертора, он обеспечивает наличие низкого уровня на выходе этого инвертора, который, в свою очередь, удерживает сигнал на выходе верхнего инвертора на высоком уровне. Но если Q имеет низкий уровень, то нижний инвертор с низким уровнем на входе вырабатывает сигнал высокого уровня на своем выходе, который вынуждает верхний инвертор иметь низкий уровень на его выходе Q; это другое устойчивое состояние. Состояние такой схемы можно было бы описать, воспользовавшись единственной переменной состояния - значением сигнала на выходе Q; возможны два состояния: Q = О и Q == 1. Этот элемент с двумя устойчивыми состояниями настолько прост, что у него нет входов, и поэтому нет возможности им управлять и изменять его состояние. Когда на схему подается напряжение питания, в ней случайно устанавливается то или другое состояние, в котором схема остается навсегда. Здесь эта схема нужна нам в качестве иллюстрации, но в разделах 8.2.3 и 8.2.4 мы приведем примеры, где она используется на самом деле. 7.1.2. Аналоговый подход Мы узнаем об элементе с двумя устойчивыми состояниями заметно больше, если рассмотрим его работу с аналоговой точки зрения. Черной линией на рис. 7.3 изображена статическая (по постоянному току) передаточная характеристика Гдля одного инвертора; выходное напряжение является функцией входного напряжения: V = 7(F). Для двух инверторов, соединенных в петлю обратной связи, как показано на рис. 7.2, имеем: V = V и F utv поэтому на одном и том же графике можно начертить передаточные характеристики для обоих инверторов, откладывая по осям координат соответствующие величины. Таким образом, черная кривая представляет собой передаточную характеристику верхнего на рис. 7.2 инвертора, а синяя кривая - передаточную характеристику нижнего инвертора. Рис. 7.2. Пара инверторов, образующих элемент с двумя устойчивыми состояниями Устойчивое равновесие Неустойчивое равновесие  Передаточные хараетеристики /Устойчивое равновесие Рис. 7.3. Передаточные характеристики инверторов в петле обратной связи с двумя устойчивыми состояниями Рассматривая только статическое поведение схемы с петлей обратной связи, но не динамические эффекты в ней, мы видим, что равновесие наступает в этой петле тогда, когда напряжения на входах и выходах обоих инверторов имеют постоянные значения, согласующиеся с требованиями, диктуемыми конфигурацией петли, и с передаточными характеристиками инверторов по постоянному току. Другими словами, должны выполняться равенства: V =V ml out2 = Щщ) и, аналогично. Воспользовавшись рисунком, можно найти точки равновесия графически - это точки, в которых пересекаются кривые, изображающие передаточные характеристики. Как ни странно, оказывается, что точек равновесия не две, а три. Две из них, отмеченные как устойчивое равновесие {stable state), соответствуют тем двум состояниям, которые мы обнаружили раньше при цифровом подходе: сигнал на выходе Q имеет значение О (низкий уровень) или 1 (высокий уровень). Третья точка, отмеченная как неустойчивое равновесие {метастабиль-яое состояние, metastable state), соответствует случаю, когда напряжения V и F находятся примерно посередине между значениями напряжений, соответствующих логической 1 и логическому 0; в этой точке ни Q, ни Q L не являются логическими сигналами в строгом смысле слова. Однако уравнения, описывающие поведение петли, удовлетворяются и в этой точке; если бы нам удалось поставить схему в состояние, соответствующее данной точке, то, теоретически, схема могла бы оставаться в этом состоянии неограниченно долго.  Устойчивое Устойчивое положение положение Даже у простейшей последовательностной схемы имеется неустойчивое равновесие, так что можете быть уверены, что этим свойством обладают все последовательностные схемы. Причем процессы, связанные с выходом из неустойчивого 7.1.3. Неустойчивое равновесие Более детальный анализ того, что происходит в точке неустойчивого равновесия, позволяет воздать должное точности названия. Равновесие в этой точке не является по-настоящему устойчивым, поскольку случайный шум будет сталкивать схему из точки неустойчивого равновесия в сторону одного из устойчивых состояний. Объясним это подробнее. Предположим, что рассматриваемая схема находится в точке неустойчивого равновесия, указанной на рис. 7.3. Предположим теперь, что из-за небольшого шума в цепи напряжение F чуть-чуть уменьшается. Это совсем малое изменение вызовет определенное увеличение напряжения F. Поскольку выходное напряжение верхнего инвертора К, является входным напряжением нижнего инвертора F2 bi можем перейти по первой горизонтальной стрелке из окрестности точки неустойчивого равновесия к другой точке на второй передаточной характеристике, согласно которой напряжение V должно иметь теперь меньшее значение и, значит, меньшим должно стать равное ему напряжение Fj. Вернемся снова к отправной точке наших рассуждений, за исключением того, что изменение напряжения Fj теперь много больше, чем то, которое бьшо вызвано шумом, и рабочая точка продолжает смещаться. Этот регенеративный процесс происходит до тех пор, пока не будет достигнуто устойчивое положение рабочей точки в верхнем левом углу нарис. 7.3. Еслижемы предпримем шумовой анализ любой из устойчивых рабочих точек, то увидим, что обратная связь возвращает схему назад к устойчивой рабочей точке, а не в сторону от нее. Неустойчивое равновесие рассматриваемой бистабильной схемы можно сравнить с поведением мяча, упавшего на вершину холма (рис. 7.4). Если мяч попадет на холм с нашей подачи, то, вероятнее всего, он немедленно скатится по ту или другую сторонулт холма. Но если мяч аккуратно поместить точно на вершину, то он будет ненадежно располагаться там до тех пор, пока из-за какого-нибудь случайного воздействия (ветер, грызуны или землетрясение) не начнется его скатывание с холма. Подобно мячу на вершине холма, наша электронная схема может оставаться в состоянии неустойчивого равновесия неопределенное время до того момента, пока она недетерминированным образом не сместится в то или в другое устойчивое состояние. Неустойчивое положение Рис. 7.4. Мяч на вершине холма в качестве иллюстрации неустойчивого равновесия ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |