
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Программные средства foundation WX г- YZ \ 00 01 11 00 Yz\ 00 П W-X F = ,X,Y,z(5.7.12,13,14,15) F = X-Z + W-X Рис. 4.31. F = lYz( 12,13,14,15): (а) карта Карно; (Ь) простые импликанты Сумма всех простых импликант называется полной суммой (complete sum). Хотя полная сумма всегда указывает допустимый способ реализации логической функции, она не всегда является минимальной. Рассмотрим, например, логическую функцию, представленную на рис. 4.32. У нее пять простых импликант, но минимальная сумма включает только три из них. Спрашивается, как можно систематически определять, какие импликанты следует брать, а какие - отбрасывать? Нужны еще два определения: Особенная клетка, содержащая 1 {distinguished l-cell), - это такая клетка, которая соответствует комбинации переменных, покрываемой только одной простой импликантой. Существенная простая импликанта {essential prime implicant) логической функции - это простая импликанта, покрывающая одну особенную клетку, содержащую 1, или большее их число. YZ\ 00 01 11 00 Yz\ 00 01 11 00 X - у w-z F = 2;w,X,Y,z(1-3A5,9,11,12,13,14,15) F = X-r + XZ + WX Рис.4.32. F = Iw> z(1.3,4,5,9,11,12,13,14,15): (a) карта Карно; (b) простые импликанты и особенные клетки, содержащие 1 Поскольку существенная простая импликанта является единственной простой импликантой, покрывающей одну из клеток, содержащих 1, она должна входить в : любую минимальную сумму данной логической функции. Таким образом, первый шаг в процедуре выбора простых импликант совсем прост: мы устанавливаем, какие из клеток, содержащих 1, являются особенными, берем соответствующие им простые импликанты и включаем их в качестве существенных простых импликант в минимальную сумму. После этого остается лишь определить, как покрыть остающиеся клетки, содержащие 1, - если таковые имеются, - не покрытые существенными простыми импликантами. В примере на рис. 4.32 три особенные клетки, содержащие 1, заштрихованы, а соответствующие им существенные простые импликанты обведены более жирными линиями. В этом примере все клетки, содержащие 1, покрываются существенными простыми импликантами, так что больше делать ничего не нужно. Аналогично обстоит дело в примере на рис. 4.33, где все простые импликанты являются существенными и поэтому все они включаются в минимальную сумму. 00 01 11 10
00 01 W-X X-Z W - Y F = %,x,Y,z(2,3,4,5,6,7,11,13,15) F = W-Y + WX + XZ + YZ Рис. 4.33. F = 1щх,уг(2. 3, 4, 5, 6, 7, 11, 13, 15): (a) карта Карно; (b) простые импликанты и особенные клетки, содержащие 1 Логическая функция, у которой не все клетки, содержащие 1, покрываются существенными простыми импликантами, приведена на рис. 4.34. Исключая существенные простые импликанты и покрываемые ими клетки, содержащие 1, мы получаем редуцированную карту, в которой имеется лишь одна клетка, содержащая 1, которую покрывают две простые импликанты. В данном случае осуществить выбор между ними легко: мы берем терм-произведение W Z, так как в нем меньше переменных и поэтому соответствующая ему логическая схема с меньшим числом входов дешевле. В более сложных случаях нам понадобится еще одно определение: О двух простых импликантах Р и Q, относящихся к редуцированной карте, говорят, что Р перекрывает {eclipses) Q (пишется: Р... Q), если Р покрывает по меньшей мере все клетки, содержащие 1, покрываемые Q. Если стоимость Р не больше, чем стоимость Q, и если Р перекрывает Q, то исключение Q из дальнейшего рассмотрения не может помешать нам найти минимальную сумму: другими словами, простая импликанта Р, по крайней мере, так же хороша, как и простая импликанта Q. WX ,- Yz\ 00 01 11 00 YZ\ 00 01 11 00 w г W-X-W-X-Y
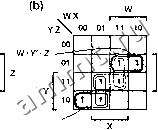
-- XY-2 F =Sw.X.y,Z<0.1.2,3,4,5,7,14,15) W-Y + W-X W-X-Y + W-2 Рис. 4.34. F = Iw,x,Yz(0,1,2,3,4,5,7,14,15): (a) карта Карно; (b) простые импли-канть( и особенные клетки, содержащие 1; (с) редуцированная карта после исключения существенных простых импликант и покрываемых ими клеток, содержащих 1 Пример перекрытия представлен на рис. 4.35. После исключения существенных простых импликант у нас остаются две клетки, содержащих 1, каждая из которых покрывается двумя простыми импликантами. Однако простая импликанта X Y Z перекрывает две другие простые импликанты, которые, таким образом, можно исключить из рассмотрения. В данном случае две клетки, содержащие 1, покрываются единственной простой импликантойX -Y- Z, которая является существенной простой импликантой второго порядка {secondary essential prime implicant) и которая должна быть включена в минимальную сумму.
 YZ\ 00 01 11
, W-X-Z W Y - Z XY-Z W-XY Р = %,Х.У.2(г.6.7.9,13,15) F = W-Y-Z * Vf-y-r * X-Y-Z Рис. 4.35. F = X,2(26,7,9,13,15): (a) карта Карно; (b) простые импликанты и особенные клетки, содержаие 1; (с) редуцированная карта после исключения существенных простых импликант и покрываемых ими клеток, содержащих 1 На рис. 4.36 показан более трудный случай: здесь у логической функции нет существенных простых импликант. Для этой функции методом проб и ошибок можно найти две различные минимальные суммы. Возможен другой систематический подход к данной проблеме, который называется л<е/ио()с!л< ветвления {branchingmethod). Начиная с любой клетки, содержа-. щей 1, мы произвольно выбираем покрывающую ее простую импликанту и вклк>-; чаем ее в наше рассмотрение, как если бы она была существенной. Это упрощает остающуюся часть задачи, которую можно решить обычным способом нахожде- ния гипотетической минимальной суммы. Этот процесс повторяется, начиная с ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||