
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Полупроводниковая схемотехнология получения отрицательного активного сопротивления. При подаче на вход положительного сигнала напряжение t/j равно t/i [это следует из формул (12.16)] и ток Jj будет положительным. Из формул (12.16) следует также, что ii = -l2= -UJR2. Таким образом, входной ток схемы будет отрицательным, хотя напряжение положительно. Следовательно, входное сопротивление схемы отрицательное: (12.17) Схема сохраняет устойчивость, пока внутреннее сопротивление источника напряжения Rl меньше сопротивления Rj- Такое же отрицательное сопротивление может быть получено, если преобразователь INIC будет включен в обратном направлении (т.е. при подключении сопротивления R на вход схемы и подаче входного напряжения на ее выход). Поскольку уравнения (12.16) удовлетворяются и для переменных токов, активное сопротивление Rj в них можно заменить полным сопротивлением Z2 и при этом также получить необходимое отрицательное полное сопротивление. Преобразователь INIC можно использовать в качестве источника напряжения с отрицательным выходным сопротивлением. Источник напряжения с напряжением холостого хода Uq и выходным сопротивлением г при наличии нагрузки выдает напряжение U = Uq - Ir.B обычном источнике Гд положительно; при увеличении нагрузки выходное напряжение будет уменьшаться. В схеме источника напряжения с отрицательным выходным со- 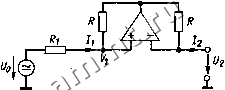 Рис. 12.25. Источник напряжения с отрицательным выходным сопротивлением. Выходное напряжение 1/2 = 1/0 + hRi. Выходное сопротивление га = -1/2 2 = -Ri. противлением, наоборот, при увеличении нагрузки напряжение U будет возрастать. Этой особенностью обладает схема на рис. 12.25. Соответствующее ей уравнение имеет вид U2=Vi = Uq- hRi. Отсюда следует, что при Jj = - Возможность использования отрицательного сопротивления распшряет границы применимости последовательного и параллельного соединения сопротивлений. Например, можно так рассчитать источник напряжения с отрицательным сопротивлением, чтобы скомпенсировать сопротивление длинной линии передачи выходного напряжения. При этом на выходе линии получим напряжение Uq с нулевым выходным сопротивлением. 12.6. ГИРАТОР Гиратор представляет собой электронную схему, которая обращает любое полное сопротивление, например преобразует индуктивность в емкость и наоборот. Эквивалентная схема гиратора приведена на рис. 12.26. Уравнения идеального гиратора имеют вид h=QUi +(l/R,)L/2, (12.18) Jj =(l/R,)L/i +0-1/2. Отсюда следует, что ток одной стороны Рис. 12.26. Символическое изображение гиратора. о- -1 i- =-0 Рис. 12.27. Эквивалентная схема реализации гиратора с помощью двух источников тока, управляемых напряжением. Рис. 12.28. Схема реализации гиратора с использованием двух преобразователей IN1C. 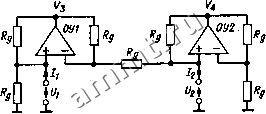 гаратора пропорционален напряжению на другой стороне гиратора. Упрощенная схема гиратора, реализованная с помощью двух управляемых напряжением источников тока, приведена на рис. 12.27. Схема гиратора на рис. 12.28 основана на двух преобразователях отрицательного сопротивления 1N1C [12.2]. Для расчета токов в этой схеме используем правило узлов для Р- и ЛГ-входов операционных усилителей ОУ 1 и ОУ 2: узел Л: (V,-Ui)/Rg-UJR + Ii = = 0, узел N,: (f3 - С/,)/Л, + (С/ - С/,)/Л, = = 0, узел Р2: {V - UVRg + (C/i - U2)/R, --/2 = 0, узел N2: {V - U2)/R,-U2/R, = 0. Исключая f3 и из этих уравнений, окончательно получим /, = U2/R, и 12 = UJR что соответствует уравнениям гиратора (12.18), приведенным выще. Рассмотрим несколько примеров прак-гаческого применения гираторов. Подключим к правым выводам гиратора резистор с сопротивлением Я. Поскольку знаки напряжения и2 И тока I2 в этом случае совпадают, получим для активного сопротивления I2 = UilR2- Подставим это выражение в рассмотренные выще уравнения. В результате получим I/, = I2R, = U2RJR2 и /i = U2IR,. Отсюда следует, что левое входное сопро-тавление R гиратора равно Rl = UJh = RllRi- (12.19) ратора обратно пропорционально сопротивлению его нагрузки. Этим свойством обладает и полное сопротивление Zi=RllZ: (12.20) На соотнощении (12.20) основано одно весьма интересное применение гиратора. Подключив к его выходу конденсатор емкостью С2, получим на другой стороне полное сопротивление z i = Rl-i(uC2, которое представляет собой не что иное, как полное сопротивление индуктивности: = RIC2. (12.21) Таким образом, входное сопротивление ги- Один из вариантов применения гираторов состоит в том, что с их помощью можно получить больщие значения индуктивно-стей, не обладающих потерями. Соответствующая эквивалентная схема показана на рис. 12.29. Относительно входа гиратор будет эквивалентен индуктивности (12.21). При Cj = 1 мкФ и Rg= \0 кОм эквивалентная - индуктивность Li будет составлять 100 Гн. Подключив параллельно этой индуктивности конденсатор С получим параллельный колебательный контур. Таким образом можно построить LwC-фильтр с высокой добротностью. Добротность параллельного колебательного контура при Ci = С2 является удобной характеристикой для оценки неидеальности практической схемы гиратора. Она называется добротностью гиратора, которая обозначается через Q. Потери в гираторе определяются двумя сопротивлениями Я , подключенными параллельно = и, Рис. 1229. Эквивалент индуктивности ----Cl \Rv Р ( 4=c, R i=/?c Рис. 12.30. а-эквивалентаая схема колебательного юнтура; 6-упрощвнная схема колебательного контура без потерь. его двум входам. При этом в схеме источника тока на рис. 12.27 параллельно соединенными оказываются входное сопротивление одного источника с выходным сопротивлением второго. В схеме с использованием двух преобразователей INIC (рис 12.28) потери связаны с тем, насколько близки значения их сопротивлений. Упрощенная схема параллельного колебательного контура, построенного с применением реального гиратора, показана на рис. 12.30,а. Используя уравнение преобразования (12.20), получим эквивалентную схему рис. 12.30,6. Отсюда находим (см. разд. 2.7), что добротность гиратора Последняя формула справедлива для низкочастотных сигналов, поскольку добротность очень чувствительна к сдвигу фаз. Из работы [12.3] получим формулу для модели первого порядка: 0(ф) =-. (1/ео) + Ф1 + Ф2 h Rg Здесь бо-значение добротности гиратора на низких частотах, а ф1 и -фазовые сдвиги между током /j и напряжением {/ 2 и током / 2 и напряжением Ц соответственно для резонансной частоты параллельного контура. При запаздывании по фазе добротность увеличивается с воз-)астанием резонансной частоты. При Ф1 + Фг! 1/Go схема становится неустойчивой и начинает генерировать колебания с резонансной частотой параллельного контура. При фазовом опережении добротность уменьшается с ростом резонансной частоты. Используя гираторы, можно выполнять преобразование не только двухполюсников, но и четырехполюсников (рис. 12.31). Для вывода уравнений воспользуемся матрицей четырехполюсника: Ац Ai2 \-Aii А22. Из формул (12.18) получаем следующее Рис. 12.31. Дуальное преобразование четырехполюсника. Рис. 12.32 Пример дуального преобразования. Уравнения преобразования: Li = RjC l2 = RjC . L3 = rlc
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |