
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Полупроводниковая схемотехнология Для дизъюнктивной нормальной формы сразу найдем максимально упрощенный результат: У = Ка + Кв + Кс + Ко, у - х2х4 + х1х3х4 + х1х3 + х1х2. 9.3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ в предыдущих разделах было показано, что любая логическая функция может быть реализована посредством соответствующей комбинации основных логических функций ИЛИ, И и НЕ. Однако имеется еще ряд логических функций, производньхх от основных, которые так часто встречаются в схемотехнике, что им были даны собственные названия. Ниже представлены их таблицы истинности и схемные обозначения. РАВНОЗНАЧНОСТЬ; при ее реализации у =\, когда значения входных переменных различны. Записывая ее дизъюнктивную нормальную форму, получим у = НЕРАВНОЗНАЧНОСТЬ (xi; Хг) = = Х1Х2 -1- Х1ЗС2. Из таблицы истинности функции неравнозначности вытекает еще одна ее особенность: эта функция совпадает с функцией ИЛИ во всех случаях, кроме одного, когда все входные переменные принимают единичное значение. Поэтому она называется также функцией ИСКЛЮЧАЮЩЕЕ ИЛИ>. Соответственно функция равнозначности называется также функцией ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ. При использовании интегральных схем иногда оказывается удобнее реализовать любые логические функции исключительно на элементах И-НЕ или ИЛИ-НЕ. При этом следует преобразовать логические функции таким образом, чтобы в них ис- Таблица 9.7 Логические функции, составляемые из функций И, ИЛИ и НЕ
функции ИЛИ-НЕ и И-НЕ образуются путем инверсии результатов, получаемых при выполнении функций ИЛИ и И соответственно. Таким образом. ИЛИ-НЕ (xi; Х2) = xi + Х2 = Х1Х2. (9.12) H-HE(xi;x2) = = Зч -t- Зс. (9.13) При реализации функции РАВНОЗНАЧНОСТЬ у = 1, если обе входные переменные равны между собой. С помощью составления дизъюнктивной нормальной формы из таблицы истинности можно получить у = РАВНОЗНАЧНОСТЬ (xi; Х2) = = JCiXj-t-Х1Х2. Функция НЕРАВНОЗНАЧНОСТЬ является отрицанием функции пользовалась только требуемая зависимость. Для этого надо сначала получить взаимосвязь между основными логическими функциями и функцией, реализуемой данной интегральной схемой. Для функции И запищем Xi.X2= Х1Х2 = H-HE(xi;x2), Х1Х2 = Х1Х2 = Xj -I- Х2 = = ИЛИ-НЕ (x-i;x2). Для функции ИЛИ также можно записать Xi -t- Х2 = xi + Х2 = ИЛИ-НЕ(xi;x2), xi -I- Х2 = Xi -I- Х2 = XiX2 = H-HE(xi; хг). Эту функцию называют также суммированием по модулю 2 (см. разд. \9.5).-Прим. перев. В табл. 9.8 показаны полученные на ос- грузочной способностью элемента (коэф-новании этих формул варианты реализа- фициентом разветвления по выходу). Коэф-ции основных логических функций. фициент разветвления по выходу, равный Таблица 9.8 Реализация основных функций с помощью элементов ИЛИ-НЕ и И-НЕ
9.4. СХЕМОТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ ОСНОВНЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ В предьщущих разделах рассматривались логические схемы без учета их внутренней структуры. Справедливость такого подхода вытекает из того, что в современной цифровой технике почти исключительно используются логические элементы, которые кроме выводов питания содержат только рассмотренные логические входы и выходы. Для реализации основных логических функций имеется ряд различных схем, которые отличаются по потребляемой мощности, напряжению питания, значениям высокого и низкого уровней выходного напряжения, времени задержки распространения сигнала и нагрузочной способности. Чтобы правильно выбрать тип схемы, необходимо по крайней мере в общих чертах знать их внутреннюю структуру. С этой целью в последующих разделах дан сравнительный анализ важнейших типов логических элементов. При соединении интегральных схем иногда к одному выходу подключается большое число входов логических элементов. Максимальное количество входов схем данного типа, подключаемых к выходу без уменьшения гарантируемого запаса помехоустойчивости, характеризуется на- 10, означает, что можно подключить 10 входов логических элементов. Если нагрузочная способность стандартного элемента оказывается недостаточной, вместо него применяют элемент с повышенной мощностью (буфер). Для логического элемента каждому входному сигналу соответствует определенный сигнал на выходе. Как было указано в гл. 8, уровень этих сигналов обозначается как высокий (Я) и низкий (L) в зависимости от того, будет ли рассматриваемое напряжение больше Ьц или меньше t/f Работа логического элемента описывается с помоцц.ю таблицы уровней 9.9. Однако по этой таблице нельзя устано- ( Таблица 9.9 Пример таблицы уровней вить, какая логическая функхдая реализована данным элементом, так как еще ничего не было сказано о соответствии между уровнем напряжения и логическим состоянием. Это соответствие произвольно; тем не менее внутри одного прибора оно выбирается однозначно. Система соответствия Н=1, L = 0 называется позитивной логикой. В данном примере она ставит в соответствие таблицу истинности 9.10, в которой легко можно Таблица 9.10 Таблица истинности в случае позитивной логики: функция И-НЕ узнать таблицу истинности функции И-НЕ. Система соответствия Н = 0, L=l называется негативной логикой. В рассматриваемом примере она дает таблицу ис-ганности 9.11, т.е. реализует функцию ИЛИ-НЕ. Таблица 9.11 Таблица истинности в случае негативной логики: функция ИЛИ-НЕ Следовательно, в зависимости от выбора логики одна и та же схема может представлять собой либо схему ИЛИ-НЕ, либо схему И-НЕ. Как правило, для задания ло-гаческих функций используется позитивная логика. При переходе к негативной логике функции меняются следующим образом: ИЛИ-НЕ < И-НЕ, ИЛИ <=>И, НЕоНЕ. 9.4.1. РЕЗИСТИВНО-ТРАНЗИСТОРНАЯ ЛОГИКА (РТЛ) Простейшим элементом РТЛ является аема ИЛИ-НЕ, представленная на рис. 9.7. Если входное напряжение имеет высокий уровень, то соответствующий транзистор открывается и на выходе формируется низкий уровень. Следовательно, в позитивной 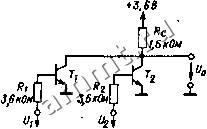 Рис. 9.7. Элемент ИЛИ-НЕ типа РТЛ. логике реализуется функция ИЛИ-НЕ. Относительно низкоомное базовое сопротивление обеспечивает полное открывание транзисторов при малом потреблении тока. Однако это приводит к весьма малой нагрузочной способности элемента. В этом отношении рассматриваемые далее схемы существенно лучше. 9.4.2. ДИОДНО-ТРАНЗИСТОРНАЯ ЛОГИКА (ДТЛ) В схеме ДТЛ, представленной на рис. 9.8, базовый ток выходного транзистора проходит через резистор Я, только в том случае, если заперты оба входных *5В 1<1 t Ш Т 4 r- +5S 1 2кОм Рис. 9.8. Элемент И-НЕ типа ДТЛ. диода Dl и D2, т.е. если все входные напряжения имеют высокий уровень. В этом случае транзистор Г, открыт и выходное напряжение находится на низком уровне. Следовательно, по позитивной логике реализуется функция И-НЕ. Ток, протекающий по резистору вызывает на двойном диоде D3 падение напряжения около 1,2 В. Вместе с напряжением на базе открытого транзистора это составит Fj = 1,2 В -Ь 0,6 В = 1,8 В. Если входное напряжение не превышает 1,2 В,
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |