
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Полупроводниковая схемотехнология полупроводниковая схемотехнология Для того чтобы избежать неясностей, кратко поясним обозначения важнейших величин. Напряжение. Напряжение между точками х и у обозначается через Uy Условимся считать напряжение Uy положительным, если точка х имеет положительный потенциал относительно точки у, и отрицательным, если точка х имеет отрицательный потенциал относительно точки у. При этом справедливо соотношение = - Uyjf. Следовательно, запись UsE- -5 В, -Use = 5 В, и ЕВ = 5В означает, что между точками Е и В приложено напряжение 5 В, причем точка Е имеет положительный потенциал относительно точки В. В схеме двойные индексы обычно опускаются и запись t/,y заменяется стрелкой напряжения U, которая направлена от точки х к точке у. Потенциал. Потенциал 7-это напряжение в точке относительно общей опорной точки 0: = ио- В схемах условным обозначением опорной точки является знак заземления. Часто используется в значении Тогда не совсем корректно говорят о напряжении точки, например анодном напряжении. Напряжение между двумя точками х и у определяется как разность Ток. Ток / в цепи условно обозначается стрелкой. Принято считать ток / положительным, если он течет в направлении, указанном стрелкой. Таким образом, ток положителен, если стрелка тока в нагрузке направлена от большего потенциала к меньшему. Как нанести стрелки тока и напряжения в схеме, несущественно, если числовые значения U и I снабжены соответствующими знаками. Если стрелки тока и напряжения в нагрузке совпадают, то, согласно закону Ома, R = U/I, если же они направлены в противоположные стороны, то Л = - U/I. Это показано на рис. 1.1. Рис. 1.1. Закон Ома. Сопротивление. Сопротивление в зависимости от напряжения или тока может определяться либо в статическом режиме R = иII, либо в режиме малых приращений сигнала {дифференциальное сопротивление) г = ди/д! AU/AI. Эти соотношения действительны при одинаковых направлениях стрелок тока и напряжения. При противоположных направлениях сопротивлению приписывается знак минус (рис. 1.1). Источник напряжения и источник тока. Для реального источника напряжения справедливо соотношение С/, = С/о - (1.1) где C/q-напряжение холостого хода (э.д.с. источника), Ri = - dt/d/a-внутреннее сопротивление источника. Это соотношение поясняет эквивалентная схема, приведенная на рис. 1.2. Ж 1а V - V Рис. 1.2. Эквивалентная схема реального источника напряжения. У идеального источника напряжения К; = = О, т. е. его выходное напряжение не зависит от тока. Другая эквивалентная схема для реального источника получается в результате преобразования уравнения (1.1) /. = (Со - U,)/R. = 1о- (1.2) где Iq = [/о/Я,-ток короткого замыкания. Эта схема приведена на рис. 1.3. Известно, что выходной ток тем меньше зависит от выходного напряжения, чем больше Rj. Предельный переход R, со приводит к идеальному источнику тока. I I i Рис. 1.3. Эквивалентная схема реального источника тока Реальный источник напряжения можно представить с помощью идеального источника напряжения (рис. 1.2) и идеального источника тока (рис. 1.3). Выбор формы представления зависит от того, является ли внутреннее сопротивление источника малым или большим по сравнению с сопротивлением нагрузки Правим узлов\ При расчете многих схем используется правило узлов, согласно которому сумма всех токов, протекающих через узел, равна нулю. При этом стрелки тока, направленные к узлу, считаются положительными, а стрелки тока, направленные от узла,-отрицательными. Использование правила узлов продемонстрируем применительно к схеме, изображенной на рис. 1.4. Пусть нужно определить напряженке U3. Для этого применим правило узлов к узлу К: О)гласно закону Ома, /,=([/! - С/з)/К  Рис. 1.4. Пример использования правила узлов. h = {U2 - итг, h=VIR. После постановки этих величин получим (t/i - [/з)/К1 + (С/2 - - = 0. В результате будем иметь С/з = (U.RR + UR,R)/{R,R + + R.R, + R2R3). Второй закон Кирхгофа. Полезным средством для расчета схем является второй закон Кирхгофа, согласно которому сумма всех напряжений замкнутой цепи равна нулю. При этом положительными считаются напряжения, направление которых совпадает с выбранным направлением тока. Напряжения противоположного направления считаются отрицательными. Следовательно, в схеме, изображенной на рис. 1.5, Цепь переменного тока. Уравнение, описывающее схему с помощью постоянных напряжений, справедливо для 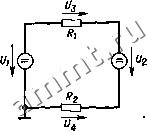 Первый закон Кирхгофа.-Ярил1. ред. Рис. 1.5. Пример использования второго закона Кирхгофа. любого зависящего от времени напряжения {t) = f{Ug (f)] при условии, что входное напряжение квазистационарно, т. е. изменяется достаточно медленно. По этой причине для обозначения как постоянных напряжений, так и напряжений любой формы будем использовать прописную букву и = U(t). Часто в уравнения для переменных напряжений не входят постоянные составляющие. В таких случаях целесообразно обозначать эти переменные напряжения строчной буквой и. Характерньп! примером переменного напряжения является напряжение синусоидальной формы: и = С/sin (юг -I- (1.3) где [/-амплитудное значение. Для характеристики синусоидальных напряжений применяется также эффективное значение 1/эфф = il/Yl или размах напряжений Uss = 2U. С целью упрощения расчета тригонометрические функции часто заменяют экспоненциальными. Формула Эйлера cos а -I- jsin а (1.4) дает возможность выразить синусоидальную функцию через комплексную экспоненциальную функцию sin а = 1ш [е }. Учитывая это, выражение (1.3) можно представить в виде и = l7Im{e< + = 1т {и e } = = Im{e* }, где и = С/e* -комплексная амплитуда. Ее модуль и\ = и\е*\= C/[cosф -I- sinфJ = U. Следовательно, он равен амплитудному значению. Аналогичные обозначения примем для токов, зависящих от времени: /, /(О, i, I, I- Эти обозначения наносятся на схемы. Направление стрелки указывает не истинную полярность величины, а ее знак. используемый при расчете, аналогично правилу, представленному на рис. 1.1 для постоянного напряжения. Для цепи переменного тока используется понятие комплексного сопротивления, которое часто называется импедансом z : Z=U/J = U-/I = = (l7 )e -- = l:Ze, где ф-фазовый сдвиг между током и напряжением. Если напряжение опережает ток, то фазовый сдвиг ф положителен. Для омического сопротивления Z = R, для емкости Z = 1 сйС = - j/aC и для индуктивности Z = jraL. Комплексные величины можно использовать в соотношениях, аналогичных законам для цепей постоянного тока [1.1, 1.2]. Комплексный коэффициент усиления определяется как А= UJU,U,e/Ueel- = = (UU,)e< -<-) = Me>, где ф-фазовый сдвиг между входным [/, и выходньп! Uj, напряжениями. Если выходное напряжение опережает входное, то фазовый сдвиг ф положителен, если отстает - отрицателен. Логарифм отношения напряжений. В электронике часто для характеристики отношения напряжений Ы = UJU используют величину, пропорциональную логарифму этого отношения: M* = 201g :201gM, которая измеряется в децибелах (дБ). Ниже приведены некоторые значения величин \А\ и \А*\: Логарифмы. Представление величин через логарифм не является однозначным. Можно, например, записать не Ig/, а 1§(/7Гц). Однако разность логарифмов Л Ig/ = = lg/2 - Ig/i определяется однозначно.
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |