Читальный зал -->  Частичная автоматизация компрессора 

1 2 3 4 5 6 [ 7 ] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91

Эта функция полностью определяет динамические и статические свойства рассматриваемого звена по каналу воздействия от

Аналогичным путем находим передаточную функцию по каналу воздействия от а к ф при неизменном р.

а{р) Тр+1

Операторные уравнения и передаточные функции удобны для структурных преобразований и решения уравнений систем при различных формах 1Входных сигналов.

Пример 3. Дифференциальное уравнение звена

15-r--l-3<f. = 21p + 18a. от

Найти передаточные функции звена по каналам воздействий р и а.

Приводим уравнение к виду (12); для этого разделим левую и правую части на коэффициент при ф

d(p

5-+9 = 7р+ 6а.

Затем из формул (23) и (24) получаем

7 6

W =- W =-

Р 5р+1 5р+1

Амплитудно-фазовая характеристика АФХ представляет собой передаточную функцию, в которой оператор р приравнен к его мнимой части /м. Физически этот метод состоит в том, что звено подвергают воздействию гармонического (синусоидального или косинусоидального) сигнала. Пусть, например, сигнал р на входе равен

р = R sin (ют + ilp).

Тогда на выходе этого звена (возникнут также - синусоидальные колебания величины ф

Ф = F sin (ют + Юф).

Очевидно, как амплитуды iR и F, так и фазы фр и фф не будут paiBHbi между собой. Их различия характеризуют статические и динамические свойства звена.

Для апериодического звена 1-го порядка АФХ можно получить из выражений (23) или (24) после подстановки в них Р = ]ш:

Избавимся от мнимого числа в знаменателе; для этого умножим числитель и знаменатель на сопряженное число (1-/юГ). Тогда

или после отделения вещественной и мнимой частей

W(/(o) = P((o)-/Q((o), (24)

Р(со) =-Q(co)=. .

Ура1внение (24) показывает, что графически АФХ можно изобразить на комплексной плоскости.

Если исключить из уравнения аТ и разрешить его относительно р((о) и Q((u), то получим

- P(co)-] + [Q(co)P = (). (25)

Это ура:внение окружности с центром в точкепо которой

Jq((jJ) скользит конец вектора исхо-

дящий из начала координат (рис. 7). Уравнение (24) в показательной фор-.p{uj ме имеет вид

WXJ(x>) = А ((о):ехр [/ф (ш)], (26)

Рис. -7. Амплитудно-фазо- () ~ lAl + шТ

вая характеристика аперио- . FT

дического звена 1-го по-

ф((o)=-arctg>Г. (28)

Как видно из рис. 7, при частоте со = О модуль вектора W{j(x)) равен у, а угол сдвига -ф = 0. По мере повышения частоты колебаний модуль стремится к нулю, а сдвиг фазы - к 90°. АФХ показывает, что звено 1-го порядка лучше воспроизводит колебания низких частот.

Пример 4. По АФХ W (jco) = ----- найти при какой частоте ампли-

1 + о/со

туда выходного сигнала уменьшится вдвое по сравнению с входным.

Л(сй)

В формулу (27) подставим-= 0,5 и, разрешив уравнение относительно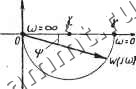

частоты, находим, что

(0=1/ - ( -1- = 0,345 рад/сек.

. Таким образом, зная параметры звена у и Т, можно с помощью переходной характеристики, передаточной функции или АФХ определить переходной процесс при возмущении звена входными сигналами различной формы.

Частным случаем апериодического звена можно считать без-инерционное или простое усилительное звено, характеризующееся тем, что Т = О и слагаемое с производной в уравнении (12) равно нулю. Следовательно, уравнение безинерционного звена совпадает по виду с уравнением (13).

Интегрирующее звено. Моделью такого звена может служить сосуд, в который подается жидкость с расходом Ущ> (рис. 8). Расход жидкости на оттоке Voi не зависит от статического столба, так как на сливной линии установлен насос Н.

Скорость подъема уровня определяется уравнением

dh Упр-Уот

где F - площадь сечения сосуда.

(29)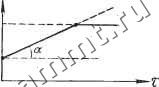

Рис. 8. Модель интегрирующего звена.

В общем виде

Рис. 9. Переходная характери стика интегрирующего звена.

(30)

(31)

(32)

Изображение этого уравнения по Лапласу

РФ (Р) - Фнач = Ъ9 (Р) + YoO (р). Тогда передаточная функция

(Р) = -. р

Передаточная функция по каналу р получится при подстановке Yp, а по каналу а - при подстановке у . Решая дифференциальное уравнение (30), нетрудно получить переходную характеристику интегрирующего звена при скачкообразном воздействии

Ф=ТЧ-ф ач- (33)

Эта характеристика представляет собой прямую линию (рис. 9), проходящую под углом к оси времени. Угол а = arctgy. В примере с сосудом Vxxp и можно в начальный момент принять равными. Тогда уровень не будет изменяться и его можно считать начальным уровнем. Если затем увеличить приток Упр на

1 2 3 4 5 6 [ 7 ] 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.