Читальный зал -->  Линейные цепи 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [ 19 ] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

Например, для графа на рис. 2.15 определитель подматрицы Ai матрицы А, соответствующей дереву 1 - 2 - 3 - 4 (см. пример 2.2),

det Ai = det

=-1.

Если образовать подматрицу Ag из столбцов 1-2 - 3 - 5 матрицы А (ветви 1 - 2 - 3 - 5 образуют подграф, содержащий контур), то

det A, = det

					-1 -

= 0.

Таким образом, если в матрице А найдены все неособенные подматрицы, то определены все деревья схемы.

Из равенства (2.16) можно доказать, что все неособенные подматрицы порядка у-1 матрицы Q также соответствуют деревьям схемы, причем определитель таких подматриц равен ± 1.

Действительно, подалатрица Q порядка у-\ матрицы Q получается в результате умножения Ад на подматрицу А порядка у-\ матрицы А: 0 = АдА, где Ад - подматрица матрицы А, соответствукяцая одному из деревьев схемы. Опре- делитель произведения двух квадратных матриц, как известно, равен произведению их определителей. Поэтому, если подматрица А соответствует любому дереву, то detA = ±l, detA == = ±1 и detQ = ±:l; если же подматрица А не соответствует дереву, то det А= О и detQ = 0.

Определители квадратных подматриц любого порядка (до - 1 включительно), образованных из матриц А или Q, могут принимать значения только -f-l, -1 и 0. Из выражения (2.17) следует, что определители квадратных подматриц любого порядка до в - у-{-\ включительно, образованных из матрицы В, могут принимать лишь значения -f 1, - 1 и 0.

Все неособенные подматрицы порядка к = в - у-\- \ матрицы В соответствуют ветвям связи (дополнениям деревьев).

Пусть выбрано одно из деревьев схемы (первое дерево) и для главных контуров, которые получаются присоединением ветвей связи к этому дереву, составлена матрица В в виде (2.17). Можно выбрать другое дерево и для другой системы главных контуров записать матрицу контуров В при условии, что порядок столбцов соответствует порядку столбцов в матрице В. Тогда матрица

В = [В Be],

где подматрица Вд(Вс) соответствует тем же ветвям, что и подматрица --F(I) в матрице (2.17), т. е. ветвям первого дерева

(ветвям связи первого дерева). По второму закону Кирхгофа,

вх+вх=о,

где Ид ( с) -матрица напряжений ветвей первого дерева (ветвей связи первого дерева). Из записанного равенства матрица

Ue = -(Be)- BX. (2.18)

Напряжение любой ветви связи может быть выражено как линейная комбинация напряжений ветвей дерева, так как существует путь по ветвям дерева между узлами ветви связи. Следовательно, в матричном соотношении (2.18) между матрицами ц. и Цд подматрица Вс должна быть неособенной, т. е. подматрица матрицы KOHtypoB, соответствующая ветвям связи любого дерева, является неособенной.

Если предположить, что Вс - неособенная подматрица порядка к матрицы В, то легко прийти к выводу, что Вс соответствует ветвям связи некоторого дерева, а Вд -ветвям дерева. В противном случае некоторые вегви, соответствующие столбцам Вд, образуют KdHTyp и число независимых уравнений, по второму закону Кирхгофа, будет больше к = в-у-\-1, что невозможно.

Таким образом, все неособенные подматрицы порядка к матрицы контуров соответствуют ветвям связи. Определители этих неособенных подматриц равны ± 1 (в случае матрицы главных контуров).

4

§ 2.4. Дуальные цепи

Дуальные графы. Дуальными называют два графа, если узловая матрица одного из них Ai равна контурной матрице другого Вз (и наоборот):

Аа = В2; (2.19)

Bi = A2. (2.20)

Из равенств (2.19) и (2.20) вытекает, что дуальные графы имеют одинаковое число ветвей. Кроме того, узлы одного графа соответствуют контурам второго и наоборот.

Для построения графа, дуального заданному, необходимо внутри каждого контура исходного графа поместить узел; один узел помещается вне графа. Затем каждую пару новых узлов соединяют ветвью так, чтобы эта ветвь пересекала ветвь исходного графа. Ориентацию ветвей нового графа производят в соответствии с рис. 2.19, на котором показаны один контур исходного графа, узел и ветви дуального графа (обозначения ветвей и узла дуального графа имеют индекс d).

Сформулированное правило иллюстрируется рис, 2.20. Исходный граф показан на рис. 2.20, а; штриховые линии соответствуют построению дуального графа. На рис. 2.20, б изображен дуальный граф.

Любому дереву исходного графа соответствуют ветви связи дерева дуального графа и наоборот. Например, дереву 1 - 2 - 3-5 (рис 2 20, а) соответствуют ветви связи 1- 2- Z- Ъ (вегви 1 - 2 - 3 - 5 образуют связи дерева 4 - 6 -7<).

Ветвям контура (сечения) исходного графа соответствуют ветви сечения (контура) дуального графа. Например, ветви 1 - 5 - 6

		4 )
	Рис. 2.19

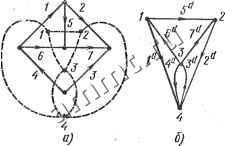Рис. 2.20

образуют контур (рис. 2.20, а); ветви 1 - 5 - 6 образуют сечение (рис. 2.20, б)

Последовательному соединению ветвей исходного графа соответствует параллельное соединение дуальных ветвей и наоборот. Например, ветви 3 и 4 соединены последовательно (рис. 2.20, а) ветви 3 и 4 -параллельно (рис. 2.20, б).

Если в некотором графе число контуров равно числу ветвей дерева: д = к, то дуальный граф имеет такую же структуру, как исходный. Такие графы называют самодуальными (рис. 2.21, а, б).

Из правила построения дуального графа можно сделать вывод-, что дуальный граф нельзя построить для любого графа. Дуальные графы существуют только для графов, которые могут быть изображены на плоскости без пересечения ветвей. Такие графы называют планарными (плоскими). Например, граф на рис. 2.15 планарный, так как он может быть изображен без пересечений ветвей (см. рис. 2.17).

На рис.. 2.22, G и б приведены примеры непланарных графов, так называемых графов Куратовского.

Дуальные элементы схемы. Двухполюсные элементы схемы называют дуальными, если зависимость и(/) одного элемента совпадает с зависимостью i{u) другого и наоборот.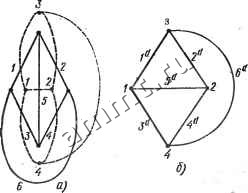

Рис. 2.21

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [ 19 ] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.