
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Линейные цепи Умножение матрицы на вектор контурных токов приводит к соотно< шениям: 1=- I - III =- ъ~7 2=I+ч 11+1v=б+ 7+в; =3 = ir+ III+ IV = e + 7 + *8; 4 = lI+lII=e-S = >: =t 7= iii; Первые четыре соотношения выражают токи ветвей дерева через контург ные токи (токи ветвей связи), остальные-токи ветвей связи, равные соответствующим контурным токам. Полученные соотношения легко составить и непосредственно по графу на рис. 2.17. Матрицы А, Q, В позволяют выразить алгебраическим языком топологию схем, что существенно при анализе сложных цепей с помощью цифровых вычислительных машин (ЦВМ). Следует определить соотношения между этими матрицами, а также ряд их свойств. Соотношения между топологическими матрицами. Если матрицы А, Q и В составлены для одного и того же графа (схемы), то они удовлетворяют следующим соотношениям: АВ = 0; (2.11) QB = 0. (2.12) Справедливость этих равенств легко показать на примерах 2.2-ь 2.4. Докажем справедливость этих равенств в общем случае. Так, вычисление произведения АВ сводится к вычислению произведений элементов матриц aijbkj и суммированию таких произведений. Произведение aijbiij отлично от нуля, если ветвь / присоединена к узлу i и входит в контур k (рис. 2.18). Но в таком случае всегда будет еще ненулевое произведение ацЬг, соответствующее ветви /, присоединенной к узлу i и принадлежащей также контуру к. При любых ориентациях ветвей /, / и контура k сумма 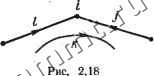 Например, для подграфа на рис. 2.18 atjbki-\-aahi = i[-l -1] -1 1 = 0. Аналогично доказывается и равенство (2.12). Если к выражениям (2.11) и (2.12) применить операцию транспонирования*, то ВА=0: BQ = 0. . (2.13) (2.14) Известно, что [ЛВС ...]=...СВА Из соотношения (2.12) вытекает справедливость отмеченного положения: если ветвям дерева присвоены первые номера, то матрицы Q и В имеют вид Q-[l F]; B = [-F 1]. Действительно, если QB = 0 и Cl==[l F], то
= [-F 1]. Целесообразно установить связь между матрицами Q, В и А. Пусть матрица А разделена на две подматрицы: А = [Ад Ае], где Ад - подматрица, соответствующая ветвям некоторого дерева; Ас - подматрица, соответствующая ветвям связи. Тогда Ai( ) = [AA] i(c) = Ад1( > + Ас1(> = 0, (2.15) где i и i- соответственно матрицы токов ветвей дерева и ветвей связи. Если подматрица дерева Ад неособенная *, то обе части уравнения (2.15) можно умножить на обратную матрицу Ад*. При этом i< 4AflAJt> = 0, , . Ця)- [1 a-aj 5(с) = Qi<> = 0* (2.16) Таким образом, матрица сечений Q = [l АдАе] = А1А, а ее подматрица, соответствующая ветвям связи, F = Ад Af>a Матрица контуров b = [-F i]=[-aUaT 1]. Как видно из равенств (2.16) и (2.17), матрицы Q и В могут быть сформированы из матрицы А. Следует подчеркнуть, что матрицы (2.16) и (2.17) записаны для главных сечений и главных контуров, соответствующих одному и тому же дереву. Единичные подматрицы в матрицах Q и В имеют различный поря- (2.17) * Неособенной назьшают квадратную матрицу, определитель которой отличен от нуля. Если Ад-неособенная матрица, то ее определитель det Ад=? О и существует матрица A~i, называемая обратной матрицей для матрицы Ад. Произведение AA=AA- = 1 (1-единичная матрица). док: в матрице Q(B) порядок единичной подматрицы равен у-Це~у+1). Неособенные подматрицы топологических матриц. Неособенные подматрицы некоторой матрицы определяют ранг, этой матрицы. Рангом матрицы называют наивысший порядок неособенной подматрицы, содержащейся в матрице. Ранг матрицы равен числу ее линейно независимых строк (столбцов). Как было показано, число линейно независимых строк матриц А, В и Q равно числу независимых уравнений, составляемых по соответствующему закону Кирхгофа. Таким образом, ранг матриц А и Q графа (схемы) равен числу ветвей дерева: Ранг матр1щы В графа (схемы) равен числу ветвей связи, т. е. к=в - у+1. Если из столбцов матрицы А образовать все возможные подматрицы порядка д = у~1, то все неособенные подматрицы порядка д матрицы А соответствуют деревьям, причем определитель таких подматриц равен ±1. Зто утверждение можно доказать в общем случае. Дерево рассматривают как самостоятельный граф и составляют для него узловую матрицу Ад. Матрица Ад - квадратная порядка д = у-1. Ранг матрицы Ад, как любой узловой матрицы, равен числу линейно независимых строк, т. е. д. Порядок матрицы Ад равен ее рангу, следовательно, матрица А неособенная. Любая неособенная подматрица, составленная из у-1 столбцов матрицы А, имеет линейно независимые столбцы. Эти столбцы могут соответствовать только ветвям дерева, поскольку столбцы матрицы А, соответствующие ветвям любого контура или подграфа, содержащего контур, на основании равенства (2.11) линейно зависимы. Таким образом, квадратная подматрица Ад порядка у-1 матрицы А является неособенной, если только столбцы Ад соответствуют дереву. Поскольку матрица Ад неособенная, т. е. ее определитель det Ад 9 О, то в матрице Ад обязательно найдется такой столбец, который содержит только, одну + 1 или только одну -1. Выполняя разложение определителя по элементам этого столбца, можно записать (1е1Ад = ±:1.Дгу, где Ау - соответствующее алгебраическое дополнение. Так как det Ад Ф- 0 то алгебраическое дополнение содержит столбец, в котором имеется только одна -f 1 (или -1). Продолжая таким образом разложение определителя, получают detA, = (±l)(±l)...(±l) = ±l. -
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |