
(926)274-88-54
Бесплатная доставка.
Бесплатная сборка.
График работы:
Ежедневно. С 8-00 до 20-00.
Почта: soft_hous@mail.ru
 |
Звоните! (926)274-88-54 Бесплатная доставка. Бесплатная сборка. |
Ассортимент тканей График работы: Ежедневно. С 8-00 до 20-00. Почта: soft_hous@mail.ru |
  
|
Читальный зал --> Электронные вычислительные машины с целью исключения систематических ошибок матрицу планирования рандомизируют с помощью таблицы случайных чисел или методом жетонов. В последнем случае число жетонов выбирают равным числу опытов (Л). Каждому жетону присваивают порядковый номер. Жетоны помещают в урну и извлекают из нее по одному. Последовательность появления жетонов определяет порядок проведения опытов. При пользовании таблицей случайных чисел выбирают любое число и случайные числа от 1 до (в нашем случае до 8) заносят в графу табл. 7.2 Номер повторения в том порядке, в котором они следуют в таблице случайных чисел. Каждое число берут только один раз.
Правильно составленная матрица планирования должна удовлетворять следующим критериям оптимальности: симметричности, нормировки и ортогональности. Симметричность относительно центра эксперимента определяется условием 2-.7=0. г=:1,2.....я, у=1,2.....N, (7.7) т. е. алгебраическая сумма элементов столбца каждого фактора (кроме Хо) равна нулю. Нормировка Заключается в том, что сумма квадратов каждого столбца равна числу точек плана матрицы: 2 l-N. (7.8) Ортогональность состоит в том, что сумма почленных произведений двух любых вектор-столбцов плана матрицы равна нулю: 2зд;-0, кф1. (7.9) Свойство ортогональности матрицы позволяет оценить коэффициенты регрессии независимо друг от друга, т. е. любой коэффициент не зависит от того, какие значения имеют другие коэффициенты. Если план матрицы отвечает этим свойствам, то он соответствует свойству ротатабельности, т. е. математическая модель, полученная в результате эксперимента, способна предсказать значения показателя параметра оптимизации с одинаковой точностью в любых направлениях на равных расстояниях от центра плана матрицы. В случае неполного квадратичного уравнения матрица ПФЭ дополняется столбцами jfj., .Xj. Т а б л и ц а 7.2
Выбор центра (основного уровня) осуществляется на основе анализа априорной информации. Интервал варьирования зависит от точности фиксирования факторов, характеристики кривизны поверхности и диапазона изменения параметров. Эксперимент проводят в соответствии с матрицей планирования. Число параллельных опытов у берут от 2 до 4 и фиксируют усилие отрыва yf. На основании этих данных определяют среднее значение усилия отрыва у/ и построчную дисперсию Sf: ~У}={уР-уТ--ЛуР)1г, (7.10) Sb2Ui-yy)/(Y-l). (7.11) Воспроизводимость эксперимента Кохрена: где Sjmax- определяют по критерию 5у raax/Ss, наибольшая из построчных дисперсий; - сумма построчных дисперсий. (7.12) Пример 7.7. Определить yj и Sj по результатам первого опыта и оценить воспроизводимость всего эксперимента (см. табл. 72). Решение. На основании формул (7.10) и (7.11) имеем 1 = (60 + 120 + 100 + 80)/4 = 90; = [(60 - 90)2 + (120 - 90)2 + (100 - 90)2 + (80 - 90)2]/3 = 666,6. Воспроизводимость эксперимента определим по формуле (7.12): 0 = 2625/8400 0,31. .Полученное значение G сравнивают с табличным (см. приложение П.П, которое определяют для выбранных уровня значимости q (обычно </=0,05), числа дублированных строк матрицы Л=8 н числа степеней свободы fi=y- -1=3. Для указанных значений Отабл=0,4377. Если 0<Отабл, то эксперимент воспроизводим и величину S2 = 2 -Sj/S ~ 1050 можно считать оценкой генеральной совокупности. Если 0>От.бл. то эксперимент невоспроизводйм. В этом случае надо увеличить число параллельных опытов или сузить интервалы варьирования, а центр плана перенести в точку с наилучшим результатом. Коэффициенты линейной математической модели н модели в виде неполного квадратичного полинома определяют по формулам: для свободного члена для коэффициента при линейных членах длч коэффициентов прн парных произведениях для коэффициентов прн тройных произведениях 1 лг (7.16) (7.17) где i, k, h - текущие номера параметров. Пример 7.2. Найти функцию связи (уравнение регрессии) для числовых значений, приведенных в табл. 7.2. Уравнение регрессии примем в виде неполного квадратичного полинома (7.2). Коэффициенты уравнении определим по формулам (7.14)...(7.17): *0 = (90 + 218,9 -Ы15 -Ь 206,2 -ь 205 -Ь 227,5 + 141,2 + 228,7)/8 = 179,1; =(-90 + 218,9 - 115 + 206,2 - 205 + 227,5-141.2 + 228.7)/8 = 41,2, В результате уравнение регрессии примет следующий вид: у= 179,1 4-41,2л:1-6,25x2+ 21,6x3 + 3,4лг,Х2- - 13,75xiX3 - 9,37х2Хз + 12,81x1X2X3. . Значимость коэффициентов оценим по критерию Стьюдента, который вычисляют для каждого коэффициента: tl = \bi\ VnTW. (7.18) Полученное значение сравним с табличным (см. приложение П.2), которое определяют для выбранного уровня значимости (обычно (7=0,05) и числа степеней свободы /2= (y-1) нлн 2 = 8(4-1) =24. При указанных знaчeнияx<тaбл=J =2,06. По формуле (7.18) вычислим <о = 179,1 /8-4/1050 = 31,3. Остальные значения критерия Стьюдента вычисляют аналогично: (о = 31,3; !, = 7,2; г2= 1,09; <з = 3,76; h2 = 0.6; 13 = 2,4; % = 1,64; 123 = 2,2. Соответствующие коэффициенты считаются значимыми, если <1Хтабл. Следовательно, коэффициенты Ьо, i, Ьз, bis, 6123 с вероятностью 0,95 значимы, а остальные незначимы. Тогда уравнение регрессии будет иметь следующий вид: у= 179,1 +41,2x1+21,6x3- 13,76x1X3+ 12,8x1X2x3. Адекватность полученной модели оценивают по критерию Фишера в такой последовательности. Дисперсия адекватности (7.19) где - значение выходного параметра для i-й строки матрицы, рассчитанное на основании полученной модели; d - число значимых членов модели. По данным табл. 7.2, 52=1110,17/3 = 370. Критерий Фншера F = SfS2 = 370/1050 = 0,35. Табличное значение критерия Фишера (см. приложение П.З) для заданного уровня значимости (7=0,05 н степеней свободы будет /2 = (Y-1)=24; fs = N-d = 3; /,абл=3. Так как f </табл, то модель адекватна. Если F>Ftz6 , гипотеза об адекватности модели отвергается. В этом слу-чае необходимо перейти к более сложному виду модели, например к полному -квадратичному полиному, нлн уменьшить шаги варьирования факторов. Полученная экспериментально-статистическая модель позволяет с вероятностью 0,95 утверждать, что на прочность термокомпрессионного соединения влияют температура и давление инструмента. Влияние времени сварки и всех взаимодействий в заданном интервале изменения первичных факторов незначительно. С увеличением числа первичных факторов резко возрастает количество опытов полного факторного эксперимента. Обычно Число первичных факторов, влияющих на выходной параметр, ле- 4-673 -97 жит в пределах 2...7. Однако в некоторых случаях их число доходит до 20, что может сделать ПФЭ нереализуемым из-за большого количества опытов. Для ускорения процесса вычисления статистических характеристик и построения модели при большом числе первичных факторов используется вычислительная техника. Алгоритм вычисления приведен на рис. 7.2. Щек матрицы эксперимента Вычисление Вычисление 5/ Вычисление 5 max Вычисление Вычисление G-критерия Проверка ё<& та5 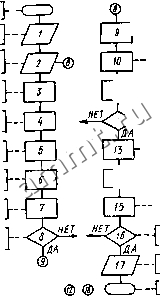 -I Ои,енка 5 Вычисление Bi ], L Г Вычисление Ц I L t-критерия Оценка значимости L Bi(h>tr] ФормароВание уравнения , регрессии ---1 Вычисление Sgg Определение F-критерия Оценка адекватности F>F mal Печать результата Останов Рис. 7.2. Схема алгоритма вычислении статистических характеристик прн ПФЭ Общее число опытов можно сократить, используя дробный факторный эксперимент, позволяющий получить линейное приближение искомой функциональной зависимости в некоторой окрест- ности базовой начальной точки при минимуме опытов. При этом для нахождения математического описания технологического процесса используется определенная часть ПФЭ: 1/2; 1/4 и т. д. Та- кие системы опытов называются дробными репликами. 7.3. Оптимизация технологических процессов на основе экспериментально-статистической модели , Оптимизация технологических процессов заключается в нахождении таких значений первичных параметров, которые позволяю? получить экстремальное (максимальное или минимальное) значение выходного параметра (критерия оптимизации). Модель технологического процесса в общем виде определяется уравнением y=/(- ii -2.-, ), (7.20) где у -выходной параметр; jfi, Х2,...,Хп - первичные факторы или входные параметры. В случае дифференцируемости функции y-xi) и неравенства нулю ее вторых производных задача оптимизации сводится к решению системы из п алгебраических уравнений вида В практике оптимизации сложных моделей технологических процессов наряду с аналитическим методом широко применяют численные методы и наиболее часто - метод крутого восхождения. Если существует несколько экстремумов, то метод крутого восхождения позволяет определить тст из них, который расположен ближе к начальным точкам. При этом находят локальное описание поверхности отклика с помощью линейного уравнения регрессии и оценивают его коэффициенты. Если модель адекватна и все коэффициенты уравнения регрессии значимы, то переходят к движению по градиенту до достижения стационарной области, в которой располагается экстремум. Если при таком движении не удается достигнуть оптимума, то ставят новую серию опытов в точке Oi с лучшим достигнутым значением параметра оптимизации, находят уравнение регрессии и на его основе определяют новое направление движения по градиенту (рис. 7.3). Такое чередование факторного планирования и движения по градиенту продолжается до достижения области оптимума, для описания которой используют планы более высоких порядков. Шаг при движении по градиенту выбирают следующим образом. Один из факторов принимают за базовый и для него вычисляют произведение соответствующего коэффициента регрессии на шаг варьирования. Для первого фактора это произведение имеет вид ftiAxi. Затем для базового фактора выбирается шаг движения по градиенту Ajfi*, с которым и будет осуществляться оптимизация. Обычно Ajfi*:Ajf/. Далее вычисляют отношение 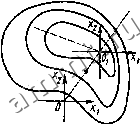 Рис. 7.3. Оптимизация по методу крутого восхождения (7.21)
ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку. Звоните! Ежедневно! (926)274-88-54 Продажа и изготовление мебели. Копирование контента сайта запрещено. Авторские права защищаются адвокатской коллегией г. Москвы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||