Читальный зал -->  Цилиндрические электромагнитные экраны 

1 2 3 4 5 6 7 8 9 [ 10 ] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

Для семейства функций F вводится новое вспомогательное обозначение

а( . У) = и{х. y)-{-ag{x, у).

где g{x, у) - произвольная функция, удовлетворяющая граничному условию g{C)=0; а -произвольный параметр соседних относительно Fo функций, для которых интеграл (1.113а) приобретает вид

/(а)=Др[( + а).

+ к, у ду

dxdy.

(1.124)

При условии, что функция имеет непрерывные производные до третьей включительно, уравнение (1.124) представляется рядом Тейлора

/(а) = /(0) + а/(0) + -/ (0) +

+ ak{a). (1.125)

Поскольку прн а=0 Ua=u{x, у), обязательным условием существования экстремума (1.113) является условие, чтобы пвая вариация была равна

8/ = а/(0) = 0. (1.126)

т. е. 8/ = а

dF , д? I

причем

,j dxdy = Q,

(1.127)

da da \ дх ) duy dg

dg dx

y~~da~~ Чу

Последние две составляющие (1.127) преобразуются по формуле Римана

(1.128)

й(С)

dxdy= (Pdx-\-Qdy), С(а)

тогда

)]\дх ди ду dUy)

дР ди.

dy -

дР ди,.

dF д

ду dUy }

) dx,dy.

Конечная форма первой вариации (1.127) при условии бы= =ай{х, у)

\ ди

JJ \ ди дх dUx а

Поскольку по условию g{C) = =0, первый из интегралов (1.129) равняется нулю, что в свою очередь позволяет сформулировать условие для функции и(х, у), приводящей функционал (1.113) к экстремуму, в виде дифференциального уравнения Эйлера

д дх

I dF

I dy\dy)

(1.130)

Можно рассмотреть четыре основных варианта функции Р.

Принцип Гамильтона. Если подынтегральная функция в (1.113) имеет форму функции Лагранжа F(u, Ых, Uy, X, у) = L(9ft, (7ft, t) = = T-V,To (1.113) будет представлять принцип Гамильтона t,

L{q q,t)dt = mm. (1.131)

Подстановкой x = t; у = 0 и (X, y)=qh{t)=u{x); u=q и =0 получается из (1.130) уравнение

Эйлера - Лагранжа для консервативных электромеханических систем [1.24]

-=0. (1.132)

Поскольку неконсервативный лангранжиан [1.24]

1ра{Т + Т,)-(у + Уо), (1.133)

получается уравнение Эйлера - Лагранжа для диссипативных электромеханических систем

д\. d	( ]	- G
dqk dt		Од,-

(1.134)

где L=T-V, причем Г- коэнер-гия или кинетическая энергия; V- потенциальная энергия; F = 1

= - S функция потерь Рей-

ли; Gk - возбуждающие силы (напряжения) [1.24].

Потенциальное поле без источников. Если в (1.113) подынтегральная функция имеет вид

? = (duldKf + {duldyf, (1.135)

то функционал примет форму

(1.135а)

Подстановкой (1.135) в (1.130) доказывается, что уравнением Эйлера для функционала (1.113а) будет уравнение Лапласа

dujdK + duldyQ. (1.136)

Потенциальное поле с источниками. Если подынтегральная функция имеет вид

F ={dujdxy + {du/dyf - 2 р {к, у),

(1.137)

то функционал в свою очередь

[/ ди \ ди

XdKdy = mm. (1.137 а)

Обязательное условие существования экстремума функционала

(1.113) в форме уравнения Пуассона получается подстановкой (1.137) в (1.130)

ди/дк + ди/ду = р(к, у). (1.138) Вихревые поля. Для подынтегральной функции

функционал

/дА\

дх )

1дАт\

rf L

(1.139)

UdA дх

dxdy -mm,

(1.139а)

и после подстановки (1.139) в (1.130) обязательное условие существования экстремума функционала (1.113) в форме диффузионного уравнения (1.36) для синусоидального изменяющегося векторного потенциала примет вид

dAjdK 4- dAJdy = аМ - цУ .

(1.140)

В общем случае решение уравнения в пространстве Q в форме д ди \ . д /. ди

ди \

= ~Q

) +

(1.141)

эквивалентно получению минимума интеграла

ди \ , , / ди \

дх )

. Ну

-\- j I - Qw dxdydz = min,

(1.142)

в обоих случаях при граничных условиях

u=u,{x,y,z) (1.143)

дх 4- а.и О,

ди , , ,

(1.144)

где Ix, ly, Iz - направляющие косинусы наружной нормали к поверхности С, ограничивающей исследуемое пространство; в тепловых задачах: q - поток тепла через единицу поверхности; аи - конвекционные потери.

Если kx=ky=kz; q=0; а=0, то (1.144) приобретает вид ди/дп- = 0.

1.6.2. Метод конечных элементов для вихревых полей. На основе п. 1.6.1 утверждается, что задачу решения дифференциального уравнения, описывающего поле (Лапласа, Пуассона и т. п.), можно заменить задачей нахождения соответствующего функционала (1.113), для которого предыдущие уравнения являются уравнениями Эйлера.

Магнитное поле синусоидально изменяющегося векторного потенциала А2=А, описанное диффузионным уравнением (1.140), можно в соответствии с (1.139) и (1.113) исследовать, решая вариационную задачу для функционала

/ дА

\ дх

fdA

Am Jfn Ащ

dxdy.

(1.145)

При этом исследуемое пространство Q (рис. 1.17) делится на конечные элементы. Для получения значений векторного потенциала Л/, Am, An в узловых точках производится минимизация функционала (1.145) с помощью вариационного метода Ритца или метода Галеркина. Процедура дискретизации пространства следующая.

Аналогично методу Ритца (1.114) усредненные значения векторного потенциала А внутри каждого элемента е аппроксимируются при помощи так называемой функции разложения в произвольной форме, например суммы многочленов высшей степени [1.36, 1.35, 1.25]. Поскольку реализация метода элементов высокого порядка весьма трудоемка [1.25], обычно ограничиваются многочленами вида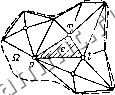

Рис. 1.17. Разделение плоского простран-стна на конечные элементы

31( * + М + СаУ)Л,] =

= (а, + + с ,1/) Ль + (а + Ьх + + сУ) А + (а + + с,у) Л =

1.Л J

(1.146)

где Aft=aft-(-&ftX-(-Cfty, причем =/, т, п.

Коэффициенты ah, Ьк, ск определяются подстановкой в (1.146) значений потенциала в узлах А{хи yi)=Ai; АЦХт, Ут) = Ага\ А{Хп, уп)=Ап, откуда получается система уравнений

У1 <,ai+bii+Ciyi)Ai-{-+ (а +й х,4-с,)Л + + (а + 6 х,+с 1/,)Л = = Л+0 + 0; для

т. Ут at-biX-\-+ с,ОЛ, + (а + йЛ +

+ c yJ4, + K + M +

+ с уЛ = 0 + Л + 0; Уп i.ai-VbiX -{-Ctyn)Ai-\-

+ (a + & x + c t/ ) Л = = 0 + 04-Л

(1.147)

1 2 3 4 5 6 7 8 9 [ 10 ] 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

ООО «Мягкий Дом» - это Отечественный производитель мебели. Наша профильная продукция - это диваны еврокнижка. Каждый диван можем изготовить в соответствии с Вашими пожеланияи (размер, ткань и материал). Осуществляем бесплатную доставку и сборку.



Звоните! Ежедневно!
 (926)274-88-54 
Продажа и изготовление мебели.

Копирование контента сайта запрещено.
Авторские права защищаются адвокатской коллегией г. Москвы.